
1. 等腰三角形的性质:
①等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴;
②等腰三角形的两个底角相等;(简称“等边对等角”)
③等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(简称“三线合一”)
师:同学们,大家都去过乐客多吧?它每天都有很多顾客,特别是到了节假日,那更是人山人海。当顾客推着满满一车物品去付款时,营业员总是能在很短的时间内告诉他应该付多少钱,为什么营业员会算得那么快呢,你知道吗? 生:因为是用计算器计算的。 师:对,今天这节课我们就来一起学习用“计算器计算”。(出示课题) 二、 学习用计算器计算 1、 认识计算器 师:你知道在我们日常生活中还有哪些地方用到了计算器吗? 生1:在菜场买菜时。 生2:在书店买书付帐时用到了计算器。 生3:工人在拿工资时也用到过计算器。 …… 师:你了解计算器吗?今天假如你是一位计算器的推销员,你打算怎样向大家介绍你手中的这款计算器的构造?(同桌之间相互说一说后再全班交流) 生(边指边说):我的计算器是英文牌子的,还有一个R,这说明是经过国家质量验证过的。这是显示器,下面是键盘,有数字键,运算符号键和功能键,它们是用三种不同的颜色来表示的。 …… 说明:各种不同的计算器的功能和操作方法也不完全相同,因此在使用前一定要先看使用说明书。但对于一些简单的操作,方法还是相同的,象开机按?关机按? 生:开机按ON/C,关机按OFF 2、 用计算器计算 师:大家已经认识了计算器,你会操作他吗?现在咱们就用计算器来算一些题目,请把计算器准备好,准备好了吗? 小黑板出示: 75+47= 24×7.6= 62.8-0.95= 师:现在请你们同桌之间说说你是怎样用计算器计算器这三题的。(同桌交流) 生1:75+47我是这样操作的,先按75再按“+”再按47,最后按“=”,显示器上就出现了结果,是112。 生2:24×7.6我是这样操作的,先按24再按“×”再按7.6,再按一下“=”结果就出来了,是182.4。 生3:62.8-0.95我是这样操作的,先按62.8再按“-”再按0.95再按“=”结果是61.85。 生4:62.8-0.95我的操作和他不一样,在按0.95时,我是先按小数点,再按9按5的。 师:是吗?我们按照这种方法试一试,看看能得到0.95吗?(学生齐操作) 师:通过计算这三题,我们可以发现,用计算器计算时只要从左往右依次按键就可以了。现在我们要来比一比谁算的最快,请准备好,开始:出示0.092÷1.15×25= 生1:我是这样操作的,先按小数点,再依次按0、9、2,再按“÷”再按1.15再按“×”再按25,最后按“=”,结果是2。 生2:我的操作方法和他基本相似,就是一开始先按0再按的小数点,结果也是2。 三、介绍计算工具的发展史 师:通过用计算器计算上面这些题目,你有什么体会?你觉得用计算器计算怎么样啊? 生1:我觉得用计算器计算很快。 生2:我觉得用计算器计算不容易出错。 生3:我觉得用计算器计算又对有快。 师:那么同学们有没有想过在计算器还没发明之前,我们的先辈们都用过哪些计算工具呢?你能不能将你课前收集的资料联系书本上的介绍来说一说?(小组交流后再全班交流) 生1:在远古时期人们是用的小石子,还有小棒。 生2:还有竹签,筷子和算盘。 生3:人们还用过算筹。 根据学生的回答板书:小石子--小棒--算筹--算盘 师:你能告诉大家什么是算筹吗? 生:算筹就是一种象筷子一样的小棒,用算筹摆出不同的形状可以表示不同的数。 师:你能不能有算筹来摆出一些数让大家猜猜呢? (学生到投影上摆出了1,2,3,9) 师:9还有不同的摆法吗?(学生上来摆)你能说说为什么你摆的是9吗? 生:上面有竖表示5,下面四横表示4,合起来就是9了。 师:这就是算筹的两种不同摆法横式和竖式。那么谁来给大家介绍一下算盘呢? 生(边指着算盘边说):这是梁,这是框和档,还有这是上珠和下珠。 然后教师在算盘上拨一个数让学生读,从而说明要先定个位后才能读数。 四、 用计算器探索规律 师:了解了计算工具的发展,并能用计算器进行计算,那么计算器还有没有其他的作用呢,下面我们就来一起探索。 用小黑板先出示: 1122÷34= 111222÷334= 11112222÷3334= 再出示:111111222222÷333334= 111…122…2÷333…34= 师:你遇到什么问题了? 生:我发现计算器已经不能把这些数显示出来了。 师:那该怎么办啊?赶快看看有没有什么规律啊?(小组合作) 生1:商3的个数和被除数中1的个数相同。 生2:商3的个数和被除数中2的个数相同。 生3:商3的个数和除数的位数相同。 生4:商3的个数比除数中3的个数多一位。 …… 师:通过这组练习你有什么体会? 生:计算器还可以帮助我们探索规律。 师:看来计算器的作用还真不小。 五、 辨证地看待计算器的使用 师:最后我们来一次比赛,分两组:一组用计算器,一组用笔算。愿意用计算器的请举手 先出示: 再出示: 3+7= 28042+13208= 2×5= 172×56= 25×4= 25144÷449= 198+2= 师:从这次比赛中,你有什么感想? 生:对于一些可以直接看出结果的题目如果用计算器计算会比较慢,而对于一些大数目的计算用计算器比较好。 师:因此,在实际应用时我们应该根据需要合理使用计算器,不可过分的依赖计算器来计算。 六、 全课总结 今天这节课我们学习了用计算器计算,你有什么体会?你觉得我们今天的学习对你有用吗,能不能说说? 七、 课堂作业 用计算器计算六道题目
1?计算下列各式:
(-3)2;(-2)3;(-4)4;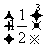 ;-0.12;
;-0.12;
-(-3)3;3·(-2)3;-6·(-3)3;-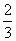 ·32;(-4)2·(-1)5?
·32;(-4)2·(-1)5?
2?填表:
3?a=-3,b=-5,c=4时,求下列各代数式的值:
(1)(a+b)2; (2)a2-b2+c2; (3)(-a+b-c)2; (4)a2+2ab+b2?
4?当a是负数时,判断下列各式是否成立?
(1)a2=(-a)2; (2)a3=(-a)3; (3)a2=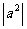 ; (4)a3=
; (4)a3=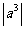 .
.
5*?平方得9的数有几个?是什么?有没有平方得-9的有理数?为什么?
6*?若(a+1)2+|b-2|=0,求a2000·b3的值?
课堂教学设计说明
1?数学教学的重要目的是发展智力,提高能力,而发展智力、提高能力的核心是发展学生的思维能力?教学中,既要注重罗辑推理能力的培养,又重注重观察、归纳等合情推理能力的培养?因此,根据教学内容和学生的认知水平,我们再一次把培养学生的观察、归纳等能力列入了教学目标?
2?数学发展的历史告诉我们,数学的发展是从三个方面前进的:第一是不断的推广;第二是不断的精确化;第三是不断的逼近?在引入新时,要尽可能使学生的学习方式与数池家的研究方式类似,不断进行推广.a2是由计算正方形面积得到的,a3是由计算正方体的体积得到的,而a4,a5,…,an是学生通过类推得到的?
推广后的结果是还要有严密的定义,让学生从更高的观点看自己推广的结果?一般来说,一个概念或一个公式形成后,要对其字母的意义、相互的关系、应用的范围逐项分析?在an中,a取任意有理数,n取正整数的说明还是必要的,要培养学生这种良好的学习习惯?
3?把学生做巩固性练习和总结运算规律放在一起进行,其效果就远远超出了巩固性练习的初衷?
我们知道,学生必须通过自己的探索才能学会数学和会学数学,与其说学习数学,不如说体验数学、做数学?始终给学生以创造发挥的机会,让学生自己在学习中扮演主动角色,教师不代替学生思考,把重点放在教学情境的设计上?例如,通过实际计算,让学生自己休会到负数与分数的乘方要加括号?
4?有理数的乘方中反映出来的数学思想主要是分类讨论思想,在例1中,精心设计了三组计算题,引导学生从底数大于零、等于零、小于零分析、归纳、概括出有理数乘方的符号法则,使学生在潜移默化中形成分类讨论思想?符号语言的使用,优化了表示分类讨论思想的形式,尤其是负数的奇次幂和偶次幂是大分类中的小分类,用符号语言就更加明显?在练习中让学生完成问题(-1)n-1,进一步巩固了分类讨论思想,使这种思想得以落实?
让学生回忆,做出小结:
1?乘方的有关概念?2?乘方的符号法则?3?括号的作用?
在小学我们已经学习过a·a,记作a2,读作a的平方(或a的二次方);a·a·a作a3,读作a的立方(或a的三次方);那么,a·a·a·a可以记作什么?读作什么?a·a·a·a·a呢?
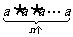 (n是正整数)呢?
(n是正整数)呢?
在小学对于字母a我们只能取正数?进入中学后,我们学习了有理数,那么a还可以取哪些数呢?请举例说明?
二讲授新课
1?求n个相同因数的积的运算叫做乘方?
2?乘方的结果叫做幂,相同的因数叫做底数,相同因数的个数叫做指数?
一般地,在an中,a取任意有理数,n取正整数?
应当注意,乘方是一种运算,幂是乘方运算的结果?当an看作a的n次方的结果时,也可以读作a的n次幂。
3.我们知道,乘方和加、减、乘、除一样,也是一种运算,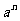 就是表示n个a相乘,所以可以利用有理数的乘法运算来进行有理数乘方的运算?
就是表示n个a相乘,所以可以利用有理数的乘法运算来进行有理数乘方的运算?
例1 计算:
(1)2,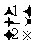 2,
2,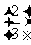 2,24; (2)-2,
2,24; (2)-2,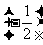 2,
2,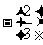 3,(-2)4;
3,(-2)4;
(3)0,02,03,04?
教师指出:2就是21,指数1通常不写?让三个学生在黑板上计算?
引导学生观察、比较、分析这三组计算题中,底数、指数和幂之间有什么关系?
(1)模向观察
正数的任何次幂都是正数;负数的奇次幂是负数,偶次幂是正数;零的任何次幂都是零?
(2)纵向观察
互为相反数的两个数的奇次幂仍互为相反数,偶次幂相等?
(3)任何一个数的偶次幂都是什么数?
任何一个数的偶次幂都是非负数?
你能把上述的结论用数学符号语言表示吗?
当a>0时,an>0(n是正整数);
当a<0时, ;
;
当a=0时,an=0(n是正整数)?
(以上为有理数乘方运算的符号法则)
a2n=(-a)2n(n是正整数);
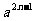 =-(-a)2n-1(n是正整数);
=-(-a)2n-1(n是正整数);
a2n≥0(a是有理数,n是正整数)?
例2 计算:
(1)(-3)2,(-3)3,[-(-3)]5;
(2)-32,-33,-(-3)5;
(3)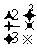 ,
,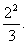 ?
?
让三个学生在黑板上计算?
教师引导学生纵向观察第(1)题和第(2)题的形式和计算结果,让学生自己体会到,(-a)n的底数是-a,表示n个(-a)相乘,-an是an的相反数,这是(-a)n与-an的区别?
教师引导学生横向观察第(3)题的形式和计算结果,让学生自己体会到,写分数的乘方时要加括号,不然就是另一种运算了?
课堂练习
计算:
(1)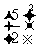 ,
,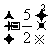 ,
,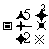 ,-
,-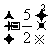 ,
,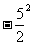 ;
;
(2)(-1)2001,3×22,-42×(-4)2,-23÷(-2)3;
(3)(-1)n-1?
2、一根绳子有10000米长,现要把它对折成长度相同的若干段,使每段刚好低于10米,则要对折多少次?
教后札记
4、若(a+1)2+|b-2|=0,求a2000·b3的值。
思考题:1、P54试一试
3、平方得9的数有几个?是什么?有没有平方得-9的有理数? 一个数的平方可能是负数吗?为什么?
必作题:P53习题1
选作题:1、P54习题2
2、当a=-3,b=-5,c=4时,求下列各代数式的值:
(1)(a+b)2; (2)a2-b2+c2; (3)(-a+b-c)2; (4)a2+2ab+b2
学生回忆,做出小结,个人发表自己的解题高招。
1.乘方的意义2、乘方的运算3、括号的作用
通过本节课的学习,结合自己的做题体会,说一说这节课中自己容易出现的问题是什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com