
1.引导学生充分进行交流,讨论与探索等教学活动,培养他们的合作与钻研精神。
采用类比平方值的求法,定义出平方根的概念,同时从这个过程可知一个什么样的数才具有平方根,这种数有几个平方根?并比较这两个平方根之间有什么关系?
2.对于任意有理数都能区分其“+”、“-”性,运用计算器已势在必行。
1.通过对平方值的计算等确立平方根的意义、开方的运算。了解算术平方根与平方根的区别与联系。毛
(三)探究拓展
6.(1)任意找一个很大正数,利用计算器将该数除以3,将所得结果再除以3…….随着运算资料的增加,你发现了什么?换一个数试试,是否仍有类似的规律?
(2)任意找一个非常大的正数,利用计算器不断地对它进行开算术平方根,你发现了什么?
(二)创新提升
5.某地开辟了一块长方形的荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2.5倍,它的面积为60000米2.
(1)试估算这块荒地的宽约为多少米?(误差小于1米)
(2)若在公园中建一个圆环喷水池,其面积为80米2,该水池的半径是多少?(精确到0.01)
(一)双基练习
1. 用计算器求出下列各式的值.
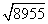
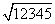 -
-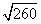
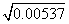
2.用计算器比较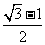 与
与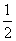 的大小.
的大小.
3.在物理学中,用电器中的电阻R与电流I,功率P之间有如下的一个关系式:P=I2R,,现有一用电器,电阻为18欧,该用电器功率为2400瓦,求通过用电器的电流I.
4.用边长为5cm的正方形纸片两张重新剪开并拼接成一个较大的正方形,其边长约为多少?(精确到0.01cm)
(三)归纳总结,知识回顾
通过本节课的学习可知,并不是所有的正数的算术平方根都是有理数,这时我们既可以用“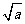 ”的形式表示,也可以用一个与
”的形式表示,也可以用一个与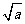 的值接近的有理数替代,于是可用计算器算出这个数,但实际上,
的值接近的有理数替代,于是可用计算器算出这个数,但实际上,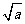 是一个无理数.
是一个无理数.
练习设计
(二)导入知识,解释疑难
1.教材内容讲解
在上学期有理数的乘方运算中,我们已经掌握了用计算器求一个数的平方的方法,现在我们要确定一个数的平方根,也可借助这种方法进行,我们不妨用计算器验证7.12,7.12=50.41,而50.41>50,故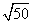 <7.1,再验证7.092=50.27>50,故7<
<7.1,再验证7.092=50.27>50,故7<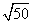 <7.09,而7.082=50.12,7.072=49.98,故7.07<
<7.09,而7.082=50.12,7.072=49.98,故7.07<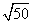 <7.08,接着继续增加小数点后一位小数,如7.071,计算7.0712=49.99,而7.0722=50.013,故7.071<
<7.08,接着继续增加小数点后一位小数,如7.071,计算7.0712=49.99,而7.0722=50.013,故7.071<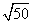 <7.072,……如此继续进行下去,可以发现将小数点后的小数位继续增加下去,一直不能穷尽,都只能使7.07……的平方值无限接近
<7.072,……如此继续进行下去,可以发现将小数点后的小数位继续增加下去,一直不能穷尽,都只能使7.07……的平方值无限接近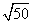 ,因此发现,
,因此发现,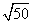 不可能化为我们以前学过的无限循环小数,只能化为无限不循环小数,而有理数只包括有限小数和无限循环小数或者整数,但
不可能化为我们以前学过的无限循环小数,只能化为无限不循环小数,而有理数只包括有限小数和无限循环小数或者整数,但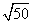 却不在这些数的范围内,只能说
却不在这些数的范围内,只能说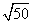 这个数不是有理数,我们把这种数重新命名为“无理数”,于是数的范围也就扩充了,是否我们可以直接用计算器来计算某一个正数的算术平方根呢?
这个数不是有理数,我们把这种数重新命名为“无理数”,于是数的范围也就扩充了,是否我们可以直接用计算器来计算某一个正数的算术平方根呢?
只要计算器上有“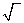 ”键或者“
”键或者“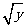 ”键,它就可以用来求某正数的算术平方根了,但不同的计算器的按键顺序不相同,只要按计算器的使用方法去按键,就可求出任意正数的算术平方根了.
”键,它就可以用来求某正数的算术平方根了,但不同的计算器的按键顺序不相同,只要按计算器的使用方法去按键,就可求出任意正数的算术平方根了.
例1:用计算器计算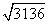 和
和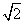 ,
,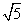 ,
,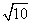 的值.
的值.
解:通过按键可得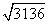 的值在计算器上显示:56,为有理数.
的值在计算器上显示:56,为有理数.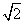 的值在计算器上显示1.414213562,而
的值在计算器上显示1.414213562,而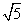 的值在计算器上显示2.236067978,
的值在计算器上显示2.236067978,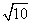 的值在计算器上显示3.16227766.从计算器上显示的数都是位数有限的,因此往往给我们一个印象“这些值都是有理数”,而事实上我们知道用平方幂验证它们的平方根时,却怎么也找不到准确的数,使其平方为2、5、10,于是我们得出:这些数不是有理数,只是一个无限不循环小数即无理数.通过计算器计算出的小数只能是这些数的算术平方根的近似值或最接近的值.运用计算器可以很方便地确定一个任意正数的算术平方根.
的值在计算器上显示3.16227766.从计算器上显示的数都是位数有限的,因此往往给我们一个印象“这些值都是有理数”,而事实上我们知道用平方幂验证它们的平方根时,却怎么也找不到准确的数,使其平方为2、5、10,于是我们得出:这些数不是有理数,只是一个无限不循环小数即无理数.通过计算器计算出的小数只能是这些数的算术平方根的近似值或最接近的值.运用计算器可以很方便地确定一个任意正数的算术平方根.
活动:怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?求出其边长.
分析:将两个面积为1的小正方形的面积相加得2,而要拼的大正方形的面积正好为2,于是可知,只要将两个小正方形剪开再重新拼合成一个正方形即能满足要求.要确定新正方形的边长,我们就得确定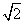 的值大约是多少,我们知道12=1,22=4,故1<
的值大约是多少,我们知道12=1,22=4,故1<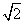 <2,也即是面积为2的正方形的边长比1大故比原小正方形的边长大,若沿原小正方形的对角线将两个小三角形剪开,得四个形状、大小完全相同的小直角三角形,将这四个直角三角形的直角边拼接起来得一个新正方形.(如课本图10.1-1)
<2,也即是面积为2的正方形的边长比1大故比原小正方形的边长大,若沿原小正方形的对角线将两个小三角形剪开,得四个形状、大小完全相同的小直角三角形,将这四个直角三角形的直角边拼接起来得一个新正方形.(如课本图10.1-1)
使用计算器不仅能很方便地计算出任意一个正数的算术平方根,而且还能使用计算器找到某些数的算术平方根之间的关系.
例3:(1)求下列各数的算术平方根.
0.000001,0.0001,0.01,1,100,10000,1000000
(2)利用计算器计算下列各式的值:
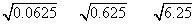
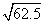
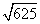
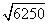
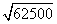 ……
……
你能找到其中的规律吗?把你的发现用自己的语言叙述出来,并利用你的发现说出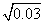 、
、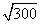 、
、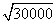 的近似值(已知
的近似值(已知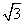 ≈1.732),你能根据
≈1.732),你能根据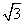 的值确定
的值确定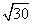 的值吗?
的值吗?
解:(1)∵0.0012=0.000001 ∴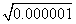 =0.001依次可得出
=0.001依次可得出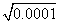 =0.01,
=0.01, 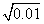 =0.1,
=0.1, 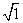 =1,
=1, 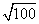 =10,
=10, 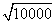 =100,
=100, 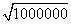 =1000
=1000
从中发现被开方数在逐渐扩大,并且每次扩大100倍,其算术平方根也在逐渐扩大,但只扩大10倍,于是猜测两个正数之间如果满足b=100a,则有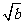 =10
=10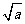 ,(或者:被开方数每扩大100倍时,其算术平方根相应地扩大10倍)
,(或者:被开方数每扩大100倍时,其算术平方根相应地扩大10倍)
(2) 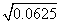 =0.25
=0.25
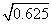 ≈0.79057
≈0.79057
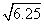 ≈7.9057
≈7.9057 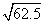 ≈7.9057
≈7.9057 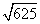 =25
=25 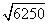 ≈79.057
≈79.057 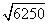 =250
=250 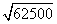 ≈790.57
≈790.57
比较相应的两列数中的被开方数及其算术平方根,同样可验证在题(1)中的规律,而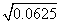 与
与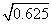 中的数开方数只扩大了10倍,它们的算术平方根之间没有规律可循.故若已知
中的数开方数只扩大了10倍,它们的算术平方根之间没有规律可循.故若已知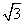 ≈1.732,可知
≈1.732,可知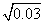 ≈0.1732,
≈0.1732, 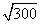 ≈17.32,
≈17.32, 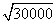 ≈173.2,但不能知
≈173.2,但不能知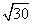 的值.
的值.
2.探究活动
(1)用一块面积为400cm2的正方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,你会怎样剪?
(2)若用上述正方形纸片剪出面积为300cm2的长方形纸片,且其长宽之比为3:2,你又怎样剪?根据你的剪法回答:只要利用面积大的纸片一定能剪出面积小的纸片吗?
解:(1)面积为400cm2的正方形纸片的边长为20cm,沿着边的方向剪出一刀,使长方形纸片的面积为300cm2,则其宽为300÷20=15cm,于是只要剪掉5cm宽的长方形纸片即可.
(2)若用上述正方形纸片剪出面积为300cm2的长方形纸片,且其长宽之比为3:2,则可设其两边为3x和2x,则有3x·2x=300,6x2=300 x2=50,x=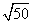 ,故长方形纸片的长为3
,故长方形纸片的长为3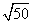 cm,宽为2
cm,宽为2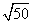 cm,而3
cm,而3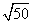 >3×7=21cm,21cm比原正方形的边长20cm更长,这是不可能的.
>3×7=21cm,21cm比原正方形的边长20cm更长,这是不可能的.
通过上述两例发现利用面积大的纸片不一定能剪出面积小的纸片.
(一)提出问题,引发讨论
在实际问题中,往往会遇到像上述情形中的问题,如果在所学过的有理数中确实找不到合适的数的平方会等于所给的数,我们该怎么表示所给数的算术平方根呢?
我们知道,若有正数x,使x2=a(a≥0),则x为a的算术平方根,记作x=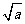 ,于是若x2=50时(x为正数),则x=
,于是若x2=50时(x为正数),则x=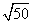 ,而72<50<82,因此有7<
,而72<50<82,因此有7<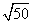 <8,现在我们就来学习如何求
<8,现在我们就来学习如何求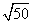 的近似值,
的近似值,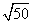 是不是有理数呢?
是不是有理数呢?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com