2.探索交流，发现规律

观察图18.1.1，你会发现右边的照片是由左边的照片放大得来．尽管它们大小不同，但形状相同．

(通过实例让学生观察相似图形的特点，感受形状相同的概念。)

图18.1.2是两张大小不同的世界地图，左边的图形可以看作是右边的图形缩小得来的．由于不同的需要，对某一地区，经常会制成各种大小的地图，但其形状(包括地图中所描绘的各个部分)肯定是相同的．

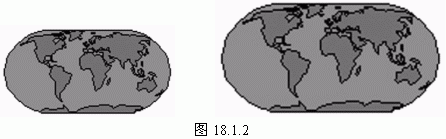
日常生活中我们会碰到很多这样形状相同、大小不一定相同的图形，在数学上，我们把具有相同形状的图形称为相似形(similar figures)．

你能说说你身边的相似形吗？请你找找看。

(让学生寻找生活中的例子，体会生活中的相似，进一步了解相似形的概念。)

　　 同一底片印出来的不同尺寸的照片也是相似图形．放电影时胶片上的图像和它映射到屏幕上的图像，都是彼此相似的．

1.创设情景，导出问题

(观察章节导图)你瞧,那些大大小小的图形是那么的相像!日常生活中,我们经常会看到这样相似的图形,那么它们有什么主要特征与关系呢?

本章将探究相似图形的特征与性质，并利用相似的性质解决实际生活中的一些问题。

(导图从生活中的人像图形的大小变化，引出相似图形，以及本章要学习的主要内容--相似图形的特征与关系，让学生带着问题进入本章的学习。)

教学重点：让学生理解相似图形概念，会判断两个图形是否相似。

3. 会判断两个图形是否相似。

2. 感受形状相同的意义，理解相似图形概念；

1. 通过生活中的实例认识物体和图形的相似；

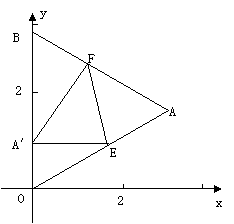
25．如图，△OAB是边长为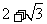的等边三角形，其中O是坐标原点，顶点B在y轴的正方向上，将△OAB折叠，使点A落在边OB上，记为A′，折痕为EF.

⑴　当A′E∥x轴时，求点A′和E的坐标；

⑵　当A′E∥x轴，且抛物线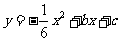经过点A′和E时，求该抛物线与x轴的交点的坐标；

⑶　当点A′在OB上运动但不与点O、B重合时，能否使△A′EF成为直角三角形？若能，请求出此时点A′的坐标；若不能，请你说明现由.

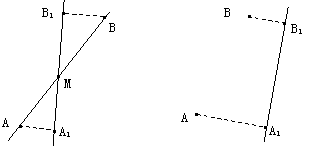
24．某供电部门准备在输电主干线l上连接一个分支线路，分支点为M，同时向新落成的A、B两个居民小区送电.已知居民小区A、B分别到主干线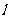的距离AA₁＝2千米，BB₁＝1千米，且A₁B₁＝4千米.

⑴　如果居民小区A、B在主干线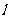的两旁，如图⑴所示，那么分支点M在什么地方时总线路最短？最短线路的长度是多少千米？

⑵　如果居民小区A、B在主干线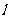的同旁，如图⑵　示，那么分支点M在什么地方时总线路最短？此时分支点M与A₁的距离是多少千米？

23．某汽车停车场预计“十·一”国庆节这天将停放大小汽车1200辆次，该停车场的收费标准为：大车每辆次10元，小车每辆次5元.根据预计，解答下面的问题：

⑴　写出国庆节这天停车场的收费金额y(元)与小车停放辆次x(辆)之间的函数关系式，并指出自变量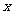的取值范围；

⑵　如果国庆节这天停放的小车辆次占停车总辆次的65%-85%，请你估计国庆节这天该停车场收费金额的范围.

22．将分别标有数字1，2，3的三张卡片洗匀后，背面朝上放在桌面上.

⑴　随机地抽取一张，求P(奇数)；

⑵　随机地抽取一张作为十位上的数字(不放回)，再抽取一张作为个位上的数字，能组成哪些两位数？恰好是“32”的概率为多少？