8. 将两个全等的不等边三角形拼成平行四边形，可拼成的不同的平行四边形的个数为______.

7.如图所示，在ABCD中，E,F分别是对角线BD上的两点，

且BE=DF，要证明四边形AECF是平行四边形，最简单的方法

是根据　　　　　　 来证明.

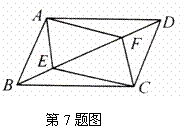
6.如图所示，ABCD中，BE⊥CD,BF⊥AD,垂足分别为

E、F，∠EBF=60°AF=3，CE=4.5，则∠C=　　　　 ，

AB=　　　　 ，BC=　　　　　 .

5.已知：四边形ABCD中，AD∥BC，要使四边形ABCD为平行四边形，

需要增加条件　　　　　　　 .(只需填上一个你认为正确的即可).

4. 在四边形ABCD中，AC与BD相交于点O，如果只给出条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形，给出以下六个说法中，正确的说法有(　　 )

(1)如果再加上条件“AD∥BC”，那么四边形ABCD一定是平行四边形；

(2)如果再加上条件“AB=CD”，那么四边形ABCD一定是平行四边形；

(3)如果再加上条件“∠DAB=∠DCB”那么四边形ABCD一定是平行四边形；

(4)如果再加上“BC=AD”，那么四边形ABCD一定是平行四边形；

(5)如果再加上条件“AO=CO”，那么四边形ABCD一定是平行四边形；

(6)如果再加上条件“∠DBA=∠CAB”，那么四边形ABCD一定是平行四边形.

A.3个　　　　　　　　　　　　　 B.4个　　　　　　　　　　　　　 C.5个　　　　　　　　　　　　　 D.6个

3.把两个全等的非等腰三角形拼成平行四边形，可拼成的不同平行四边形的个数为(　　　 )

A.1　　 B.2　　 C.3　　 D.4

2.已知：四边形ABCD中，AD∥BC，分别添加下列条件之一：①AB∥CD；② AB=CD, ③AD=BC，④∠A=∠C，⑤∠B=∠D，能使四边形ABCD成为平行四边形的条件的个数是(　　 )

A.4　　　 B.3　　 C.2　　 D.1

1.下列条件中不能判定四边形ABCD为平行四边形的是(　　　　 )

A.AB=CD,AD=BC　　　　　　　 B.AB∥CD，AB=CD

C.AB=CD ，AD∥BC　　　　　　 D. AB∥CD，AD∥BC

12. 解：(1)有4对全等三角形．　　

　　 分别为△AMO≌△CNO，△OCF≌△OAE，△AME≌△CNF，△ABC≌△CDA．

　　 (2)证明：∵OA=OC，∠1=∠2，OE=OF，

　　 ∴△OAE≌△OCF，∴∠EAO=∠FCO．　

　　 在ABCD中，AB∥CD，

∴∠BAO=∠DCO，∴∠EAM=∠NCF．　　

课时三平行四边形的判定(一)

11.证明：∵DE∥AB，DF∥AC

∴四边形AEDF是平行四边形，∴DF=AE，又∵DE∥AB，∴∠B=∠EDC，又∵AB=AC,∴∠B=∠C，∴∠C=∠EDC，∴DE=CE，∴DF+DE=AE+CE=AC=AB.