2．课前热身

　　 (1)(师手拿一支大三角形)请同学们也拿也一支与我一样的三角板，这两个三角板的三个内角有何关系？它们全等吗？这说明了什么？

　　 (2)如果已知两个三角形有两边和一角对应相等，应分几种情形讨论？

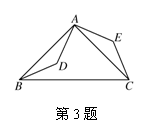
3.如图,点D是等腰直角三角形ABC内一点,AB＝AC,将△ABD绕点A逆时针旋转90°,点D与点E重合,则△ABD≌_________,　AD＝_________,　BD＝_________.

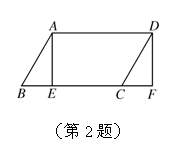
2.如图,AE是平行四边形ABCD的高,将△ABE沿AD方向平移,使点A与点D重合,点E与点F重合,则△ABE≌_________,　∠F＝_________°.

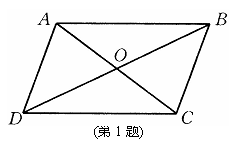
1.如图,点O是平行四边形ABCD的对角线的交点,△AOB绕O旋转180º,可以与△___________重合,这说明△AOB≌△___________.这两个三角形的对应边是AO与__________,OB与__________,BA与__________;对应角是∠AOB与________,∠OBA与_________,∠BAO与___________.

2.如果两个三角形有两组对应相等的元素(边或角),那么这两个三角形一定全等吗？想一想,会有几种可能的情况？分别按照下面的条件,用刻度尺或量角器画三角形,并和周围的同学比较一下,所画的图形是否全等.

(1)　三角形的两个内角分别为30°和70°;

(2)　三角形的两条边分别为3cm和5cm;

(3)　三角形的一个内角为60°,一条边为3cm;

(i)　这条长3cm的边是60°角的邻边;

(ii)　这条长3cm的边是60°角的对边.

你一定会发现,如果只知道两个三角形有一组或两组对应相等的元素(边或角),那么这两个三角形不一定全等(甚至形状都不相同).

思 考

如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况？这时,这两个三角形一定会全等吗？

练习

1.我们从最简单的开始,如果只知道两个三角形有一组对应相等的元素(边或角),这两个三角形一定全等吗？

(1)　如果只知道两个三角形有一个角对应相等,那么这两个三角形全等吗？

(2)　如果只知道两个三角形有一条边对应相等,那么这两个三角形全等吗？

1．复习导入

我们知道：　若两个三角形的三条边、三个角分别对应相等,则这两个三角形全等.那么能否减少一些条件,找到更为简便的判定三角形全等的方法？

显然由于三角形的内角和等于180°,如果两个角分别对应相等,那么另一个角必然也相等.这样,若两个三角形的三条边、两个角分别对应相等,则这两个三角形仍然全等.

能否再减少一些条件？对两个三角形来说,六个元素(三条边、三个角)中至少要有几个元素分别对应相等,两个三角形才会全等呢？

　　 通过画图的方式探索两个三角形全等的识别方法之(SAS)，弄清“已知三个角”和“已知两边和其中一边的对角”的不可识别的原因．

4． 连结BC．

△ABC即为所求．

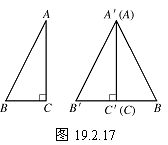
如图19．2．17，在Rt△ABC和Rt△A′B′C′中，已知∠ACB＝∠A′C′B′＝90°， AB＝A′B′， AC＝A′C′．

由于直角边AC＝A′C′，我们移动其中的Rt△ABC，使点A与点A′、点C与点C′重合，且使点B与点B′分别位于线段A′C′的两侧．因为∠ACB＝∠A′C′B＝∠A′C′B′＝90°，故∠B′C′B＝∠A′C′B′+∠A′C′B＝180°，因此点B、C′、B′在同一条直线上．于是在△A′B′B中，由AB＝A′B＝A′B′(已知)，得∠B＝∠B′．由“角角边”，便可知这两个三角形全等．于是可得

如果两个直角三角形的斜边和一条直角边分别对应相等，那么这两个直角三角形全等．简记为H．L．(或斜边直角边)．

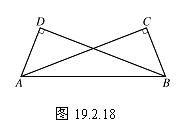例4如图19．2．18，已知AC＝BD， ∠C＝∠D＝90°，求证Rt△ABC≌Rt△BAD．

证明∵ ∠C＝∠D＝90°，

∴ △ABC与△BAD都是直角三角形．

在Rt△ABC与Rt△BAD中，

∵ AB＝BA，

AC＝BD，

∴ Rt△ABC≌Rt△BAD(H．L．).

3． 以点B为圆心，以5cm长为半径画圆弧，交射线AM于点C；