2．能运用平行四边形的性质与判定定理进行比较简单的综合推理与证明．

　　 基础与巩固

1．会证明平行四边形的判定定理，结合具体命题了解反证法．

20.1 平行四边形的判定 同步练习

　　 目标与方法

3、二次函数y=ax²+bx+c何时为一元二次方程?

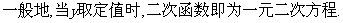
布置作业：72页 1、2

2、一元二次方程ax²+bx+c=0与二次三项式ax²+bx+c及二次函数y=ax²+bx+c这三个“二次”之间互相转化的关系.体现了数形结合的思想

1、若一元二次方程ax²+bx+c=0的两个根是x₁、x₂，　 则抛物线y=ax²+bx+c与x轴的两个交点坐标分别是A(x₁，0　 )，　 B( x₂，0 )

6、抛物线y=ax²+bx+c(a≠0)的图象全部在轴下方的条件是(　　 )

(A)　　 a＜0　 b²-4ac≤0(B)a＜0　 b²-4ac＞0

(B)　　 (C)a＞0　 b²-4ac＞0 (D)a＜0　 b2-4ac＜0

想一想

在本节一开始的小球上抛问题中，何时小球离地面的高度是60 m？你是怎样知道的？

学生交流：在式子h =－5t ²+v ₀t +h ₀中v ₀为40m/s， h ₀=0，h=60 m，代入上式得

　　 －5t ²+40t=60

　　 t ²–8t+12=0

∴t=2或t=6

因此当小球离开地面2秒和6秒时，高度是60 m.

课堂练习　 72页

小结：本节课学习了如下内容：

5. 已知抛物线 y=-2(x+1)²+8　 ①求抛物线与y轴的交点坐标;②求抛物线与x轴的两个交点间的距离.

4、已知抛物线y=x²+px+q与x轴的两个交点为(-2，0)，(3，0)，则p=　　 ，q=　　　 .

3、已知抛物线y=x²-3x+a+1与x轴最多只有一个交点，则a的范围是　　　　　　 .