
(一)湖州市中考试卷中关于函数内容的分析
|
|
2000 |
2001 |
2002 |
2003 |
2004 |
|||||
|
题数 |
分值 |
题数 |
分值 |
题数 |
分值 |
题数 |
分值 |
题数 |
分值 |
|
|
选择题 |
3 |
9 |
2 |
6 |
2 |
6 |
4 |
12 |
2 |
6 |
|
填空题 |
1 |
3 |
0 |
0 |
1 |
3 |
1 |
3 |
2 |
6 |
|
解答题 |
2 |
17 |
3 |
19 |
2 |
16 |
1 |
12 |
1 |
10 |
|
自选题 |
|
|
|
|
|
|
|
|
1 |
4 |
|
与整卷比 |
6/27 |
24% |
5/27 |
21% |
5/27 |
20% |
6/26 |
22% |
6/28 |
20% |
由上表可以看出:
(1)函数知识在近五年考试中,题量与所占分值相对比较稳定,题量一般在5-6题,分值一般在25分左右,题量与分值占整卷的20%左右.
(2)函数知识在选择题、填空题、解答题中均有出现. 基础综合题(填空、选择题)的总分值一般略高于一定难度的综合题的总分值;基础综合题的题数多于综合题的题数.
25.若P为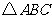 所在平面上一点,且
所在平面上一点,且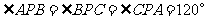 ,则点
,则点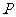 叫做
叫做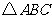 的费马点.
的费马点.
 (1)若点
(1)若点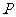 为锐角
为锐角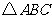 的费马点,且
的费马点,且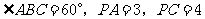 ,则
,则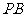 的值为________;
的值为________;
(2)如图,在锐角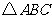 外侧作等边
外侧作等边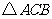 ′连结
′连结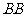 ′.
′.
求证: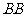 ′过
′过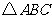 的费马点
的费马点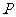 ,且
,且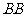 ′=
′=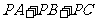 .
.
浙江省2009年初中毕业生学业考试(湖州市)
24.(本小题12分)
已知抛物线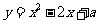 (
(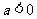 )与
)与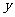 轴相交于点
轴相交于点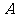 ,顶点为
,顶点为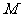 .直线
.直线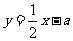 分别与
分别与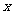 轴,
轴,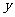 轴相交于
轴相交于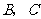 两点,并且与直线
两点,并且与直线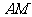 相交于点
相交于点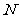 .
.
(1)填空:试用含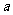 的代数式分别表示点
的代数式分别表示点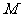 与
与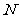 的坐标,则
的坐标,则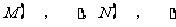 ;
;
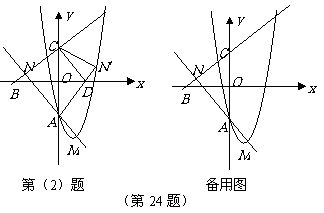
(2)如图,将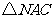 沿
沿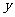 轴翻折,若点
轴翻折,若点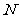 的对应点
的对应点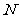 ′恰好落在抛物线上,
′恰好落在抛物线上,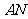 ′与
′与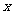 轴交于点
轴交于点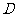 ,连结
,连结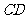 ,求
,求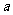 的值和四边形
的值和四边形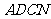 的面积;
的面积;
(3)在抛物线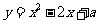 (
(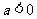 )上是否存在一点
)上是否存在一点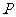 ,使得以
,使得以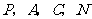 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出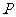 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
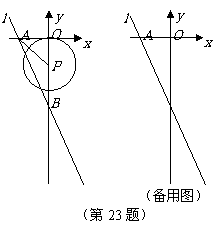
23.(本小题10分)
如图,在平面直角坐标系中,直线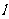 ∶
∶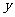 =
=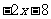 分别与
分别与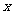 轴,
轴,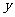 轴相交于
轴相交于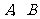 两点,点
两点,点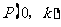 是
是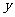 轴的负半轴上的一个动点,以
轴的负半轴上的一个动点,以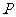 为圆心,3为半径作
为圆心,3为半径作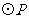 .
.
(1)连结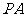 ,若
,若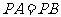 ,试判断
,试判断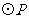 与
与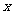 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(2)当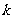 为何值时,以
为何值时,以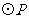 与直线
与直线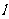 的两个交点和圆心
的两个交点和圆心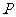 为顶点的三角形是正三角形?
为顶点的三角形是正三角形?
22.(本小题10分)
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量达到100辆.
(1) 若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2009年底家庭轿车将达到多少辆?
(2) 为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
21.(本小题10分)
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为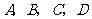 四等,并绘制成下面的频数分布表和扇形统计图.
四等,并绘制成下面的频数分布表和扇形统计图.

(1)试直接写出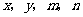 的值;
的值;
(2)求表示得分为 等的扇形的圆心角的度数;
等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到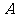 等和
等和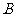 等的人数共有多少人?
等的人数共有多少人?
20.(本小题8分)
如图:已知在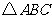 中,
中,
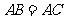 ,
, 为
为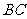 边的中点,过点
边的中点,过点 作
作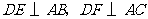 ,
,
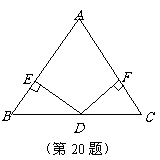 垂足分别为
垂足分别为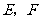 .
.
(1)
求证: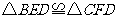 ;
;
(2)若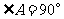 ,求证:四边形
,求证:四边形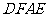 是正方形.
是正方形.
19.(本题有2小题,每小题5分,共10分)
(1)计算: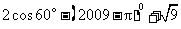
(2)解方程: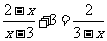
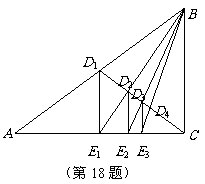
18.如图,已知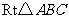 ,
,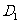 是斜边
是斜边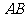 的中点,
的中点,
过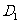 作
作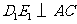 于
于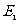 ,连结
,连结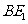 交
交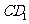 于
于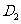 ;
;
过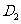 作
作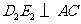 于
于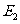 ,连结
,连结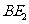 交
交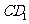 于
于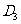 ;
;
过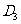 作
作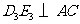 于
于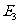 ,…,如此继续,可以依次得到点
,…,如此继续,可以依次得到点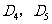 ,…,
,…,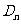 ,分别记
,分别记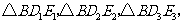 …,
…,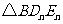 的面积为
的面积为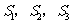 ,…
,…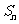 .则
.则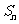 =________
=________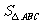 (用含
(用含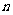 的代数式表示).
的代数式表示).
17. 已知抛物线
已知抛物线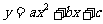 (
(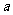 >0)的对称轴为直线
>0)的对称轴为直线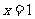 ,且经过点
,且经过点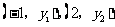 ,试比较
,试比较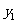 和
和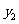 的大小:
的大小:
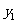 _
_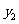 (填“>”,“<”或“=”)
(填“>”,“<”或“=”)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com