
1.(2008年浙江省衢州市)为参加电脑汉字输入比赛,甲和乙两位同学进行了6次测试,成绩如下表:
甲和乙两位同学6次测试成绩(每分钟输入汉字个数)及部分统计数据表

有四位同学在进一步算得乙测试成绩的方差后分别作出了以下判断,其中说法正确的是( )
A、甲的方差大于乙的方差,所以甲的成绩比较稳定;
B、甲的方差小于乙的方差,所以甲的成绩比较稳定;
C、乙的方差小于甲的方差,所以乙的成绩比较稳定;
D、乙的方差大于甲的方差,所以乙的成绩比较稳定;
答案:C
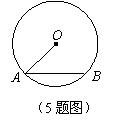
5.(15)(2008年遵义市)如图,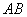 是
是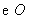 的弦,半径
的弦,半径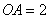 ,
,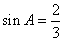 ,则弦
,则弦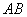 的长为( D
)
的长为( D
)
A.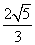 B.
B.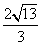 C.4 D.
C.4 D.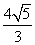
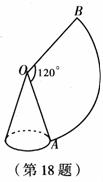
(16)(2008年山西省)如图,有一圆心角为120 o、半径长为6cm的扇形,若将OA、OB重合后围成一圆锥侧面,那么圆锥的高是( A )
 A.
A.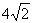 cm
cm
B.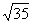 cm
cm
C.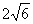 cm
cm
D.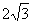 cm
cm
(17)(2008年衢州)如图,点O在Rt△ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,
O
连结OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么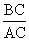 的值约为(
的值约为(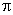 取3.14) ( C
)
取3.14) ( C
)
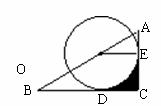
A、2.7 B、2.5 C、2.3 D、2.1
(18) (2008年衢州)一个圆锥侧面展开图的扇形的弧长为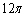 ,则这个圆锥底面圆的半径为( A )
,则这个圆锥底面圆的半径为( A )
A.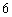 B.
B.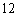
C. D.
D.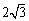
 (19)(08眉山)如图,等边
(19)(08眉山)如图,等边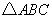 的边长为12cm,内切
的边长为12cm,内切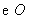 切
切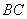 边于
边于 点,则图中阴影部分的面积为( A )
点,则图中阴影部分的面积为( A )
A.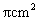 B.
B.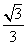
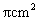
C.2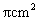 D.
D.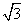
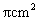
(21)(2008年南通市)在一次数学探究型学习活动中,某学习小组要制作一个圆锥体模型,操作规则是:在一块边长为16cm的正方形制片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面.它们首先设计了如图所示的方案一,发现这种方案不可行,于是他们调整了扇形和圆的半径,设计了如图所示的方案二.(两个方案的图中,圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切)
(1)请说明方案一不可行的理由;
(2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由.
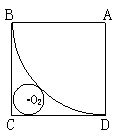
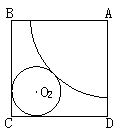
方案一 方案二
解:(1)理由如下:
∵扇形的弧长=16×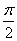 =8π,圆锥底面周长=2πr,∴圆的半径为4cm.
=8π,圆锥底面周长=2πr,∴圆的半径为4cm.
由于所给正方形纸片的对角线长为16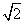 cm,而制作这样的圆锥实际需要正方形直劈昂的对角线长为16+4+4
cm,而制作这样的圆锥实际需要正方形直劈昂的对角线长为16+4+4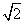 =(20+4
=(20+4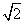 )cm,20+4
)cm,20+4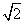 >16
>16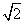 ,
,
∴方案一不可行.
(2)方案二可行.求解过程如下:
设圆锥底面圆的半径为rcm,圆锥的母线长为Rcm,则
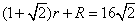 ,① 2πr=
,① 2πr=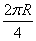 .②
.②
由①②可得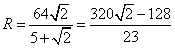 ,r=
,r=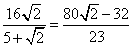 .
.
故所求圆锥的母线长为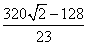 cm,底面圆的半径为
cm,底面圆的半径为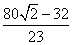 cm.
cm.
(22)(2008乌鲁木齐).如图9,在平面直角坐标系中,以点 为圆心,2为半径作圆,交
为圆心,2为半径作圆,交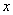 轴于
轴于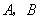 两点,开口向下的抛物线经过点
两点,开口向下的抛物线经过点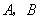 ,且其顶点
,且其顶点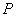 在
在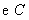 上.
上.
(1)求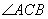 的大小;
的大小;
(2)写出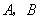 两点的坐标;
两点的坐标;
(3)试确定此抛物线的解析式;
(4)在该抛物线上是否存在一点 ,使线段
,使线段 与
与 互相平分?若存在,求出点
互相平分?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
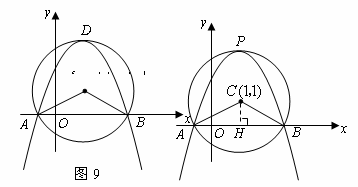
解:(1)作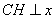 轴,
轴,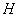 为垂足,
为垂足,
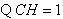 ,半径
,半径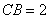
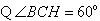 ,
,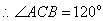
(2)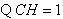 ,半径
,半径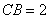
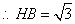 ,故
,故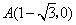
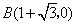
(3)由圆与抛物线的对称性可知抛物线的顶点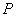 的坐标为
的坐标为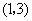
设抛物线解析式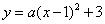
把点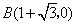 代入上式,解得
代入上式,解得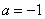
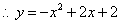
(4)假设存在点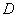 使线段
使线段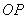 与
与 互相平分,则四边形
互相平分,则四边形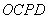 是平行四边形
是平行四边形
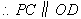 且
且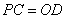 .
.
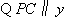 轴,
轴, 点
点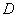 在
在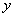 轴上
轴上
又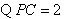 ,
,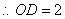 ,即
,即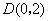 .
.
又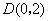 满足
满足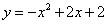 ,
,
 点
点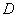 在抛物线上
在抛物线上
所以存在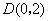 使线段
使线段 与
与 互相平分
互相平分
(23)(2008年辽宁省十二市) 20.如图10,
20.如图10,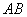 为
为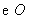 的直径,
的直径,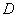 为弦
为弦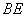 的中点,连接
的中点,连接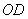 并延长交
并延长交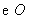 于点
于点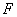 ,与过
,与过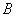 点的切线相交于点
点的切线相交于点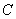 .若点
.若点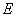 为
为 的中点,连接
的中点,连接 .
.
求证: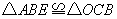 .
.
.解析:本题主要考查圆的有关知识及三角形全等的判定方法的掌握,一定要充分运用圆的相关知识,得到相等的线段和角,然后根据三角形全等的判定方法进行判定即可.
解:(1)证明:如图2.
 是
是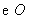 的直径.
的直径.

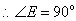
又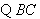 是
是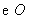 的切线,
的切线,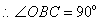
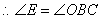
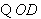 过圆心,
过圆心,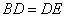 ,
,
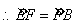
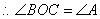 .
.
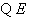 为
为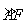 中点,
中点,
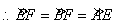

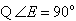
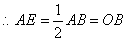
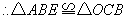 .
.
(24)(2008年贵阳市)如图10,已知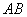 是
是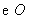 的直径,点
的直径,点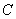 在
在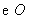 上,且
上,且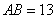 ,
,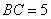 .
.
(1)求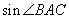 的值.(3分)
的值.(3分)
(2)如果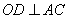 ,垂足为
,垂足为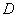 ,求
,求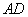 的长.(3分)
的长.(3分)
(3)求图中阴影部分的面积(精确到0.1).(4分)


答案:(1)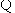 AB是⊙O的直径,点C在⊙O上
AB是⊙O的直径,点C在⊙O上
 ∠ACB = 90o
∠ACB = 90o
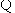 AB=13,BC=5
AB=13,BC=5
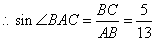 .
.
(2)在Rt△ABC中,
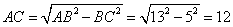 .
.
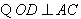 ,
,
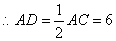 .
.
(3)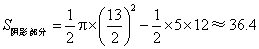 (平方单位)
(平方单位)
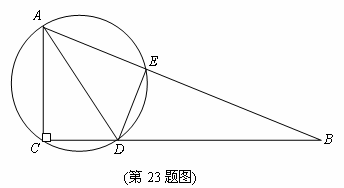
(25)(2008陕西)如图,在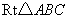 中,
中,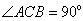 ,
,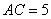 ,
,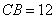 ,
,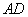 是
是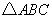 的角平分线.过
的角平分线.过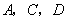 三点的圆与斜边
三点的圆与斜边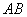 交于点
交于点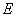 ,连接
,连接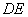 .
.
(1)求证: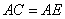 ;
;
(2)求 外接圆的半径.
外接圆的半径.
(1)证明: ,
,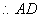 为直径
为直径
又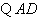 是
是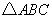 的角平分线,
的角平分线,
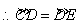 ,
,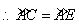 .
.

(2)解: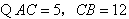 ,
,
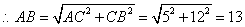 .
.
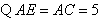 ,
,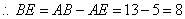 .
.
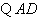 为直径,
为直径,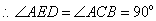 .
.
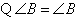 ,
,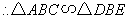
 .
.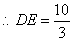 .
.
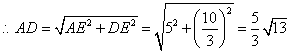 .
.
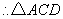 外接圆的半径为
外接圆的半径为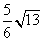
(26)(2008年龙岩市)如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.
(1)判断直线DC与⊙O的位置关系,并给出证明;
(2)设点D的坐标为(-2,4),试求MC的长及直线DC的解析式.
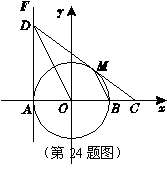
答案:(1)答:直线DC与⊙O相切于点M .
证明如下: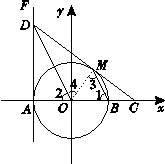 连OM, ∵DO∥MB,
连OM, ∵DO∥MB,
∴∠1=∠2,∠3=∠4 .
∵OB=OM,
∴∠1=∠3 .
∴∠2=∠4 .
在△DAO与△DMO中,
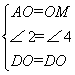
∴△DAO≌△DMO . ∴∠OMD=∠OAD .
由于FA⊥x轴于点A,∴∠OAD=90°.
∴∠OMD=90°. 即OM⊥DC
∴DC切⊙O于M.
(2)解:由D(-2,4)知OA=2(即⊙O的半径),AD=4
由(1)知DM=AD=4,由△OMC∽△DAC,知= = = .
∴AC=2MC.
在Rt△ACD中,CD=MC+4.
由勾股定理,有(2MC)2+42=(MC+4)2,解得MC= 或MC=0(不合,舍去).
∴MC的长为.
∴点C(,0).
设直线DC的解析式为y = kx+b
则有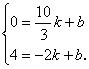
解得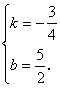
∴直线DC的解析式为 y =-x+.
.
(27)(2008年江苏省迁宿市)如图,⊙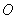 的直径
的直径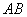 是
是 ,过
,过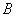 点的直线
点的直线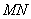 是⊙
是⊙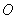 的切线,
的切线,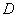 、
、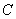 是⊙
是⊙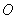 上的两点,连接
上的两点,连接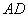 、
、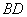 、
、 和
和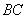 .
.
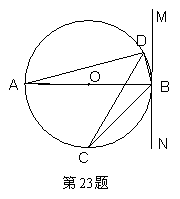
(1)求证: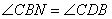 ;
;
(2)若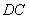 是
是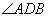 的平分线,且
的平分线,且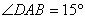 ,求
,求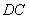 的长.
的长.
17.(10)(2008年遵义市)如图,梯形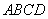 中,
中,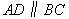 ,
,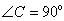 ,
,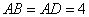 ,
,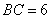 ,以
,以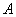 为圆心在梯形内画出一个最大的扇形(图中阴影部分)的面积是
为圆心在梯形内画出一个最大的扇形(图中阴影部分)的面积是 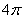 . .
. .

(11)(2008年龙岩市)如图,量角器外沿上有A、B两点,它们的读数分别是70°、40°,则∠1的度数为
15° . 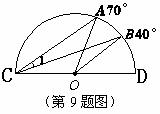
▲
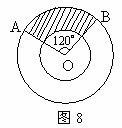
(12)(2008年江苏省迁宿市)用圆心角为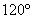 ,半径为
,半径为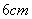 的扇形做成一个无底的圆锥侧面则此圆锥的底面半径为:2cm
的扇形做成一个无底的圆锥侧面则此圆锥的底面半径为:2cm
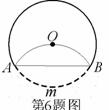
(13) (2008湖北省荆门)如图,将圆沿AB折叠后,圆弧恰好经过圆心,则( c ) 等于
(A) 60°. (B) 90°. (C)120°. (D)150°.
(13)(湖南邵阳)计算机把数据存储在磁盘上,磁盘上有一些同心圆转道.如图(九),现有一张半径为45毫米的磁盘,磁盘的最内磁道半径为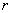 毫米,磁盘的最外圆周不是磁道,磁道上各磁道之间的宽度必须不小于0.3毫米,这张磁盘最多有
毫米,磁盘的最外圆周不是磁道,磁道上各磁道之间的宽度必须不小于0.3毫米,这张磁盘最多有 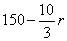 条磁道.
条磁道.

(14)(湖南常德)小红量得一个圆锥的母线长为15㎝,底面圆的直径是6㎝,它的侧面积为 45π㎝2(结果保留π).
11.(1)(2008年镇江市)圆柱的底面半径为1,母线长为2,则它的侧面积为 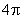 (结果保留
(结果保留 ).
).
(2)(2008年衢州)在半径为5的圆中,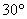 的圆心角所对的弧长为___
的圆心角所对的弧长为___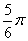 .___(结果保留
.___(结果保留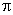 )
)
(3)在(2008年衢州)半径为5cm的圆中,两条平行弦的长度分别为6cm和8cm,则这两条弦之间的距离为 1cm或7cm .
(4)(2008乌鲁木齐)如图4所示的半圆中,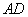 是直径,且
是直径,且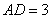 ,
,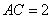 ,
,
则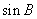 的值是
的值是 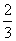 .
.
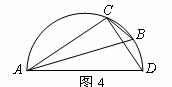
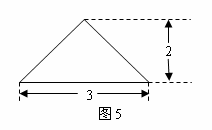
(5)(2008乌鲁木齐)如图5所示是一个圆锥在某平面上的正投影,则该圆锥的侧面积是 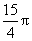 .
.
(6)(2008衢州)在半径为5的圆中,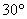 的圆心角所对的弧长为____
的圆心角所对的弧长为____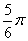 ._____
._____
(结果保留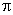 )
)
(7)(2008年辽宁省十二市)一个圆锥底面周长为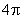 cm,母线长为5cm,则这个圆锥的侧面积是
cm,母线长为5cm,则这个圆锥的侧面积是 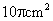 .
.
(8)(2008年山西省太原市)已知圆锥的底面半径为2cm,母线长为4cm,则圆锥的侧面积为: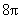 cm2.
cm2.
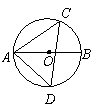 (9)(2008年山西省太原市)如图,
(9)(2008年山西省太原市)如图,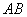 是
是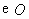 的直径,
的直径, 是
是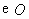 的弦,连接
的弦,连接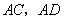 ,
,
若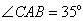 ,则
,则 的度数为 .
的度数为 .
答案:55°
5.(30)(2008年遵义市)如图,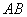 是
是 的弦,半径
的弦,半径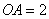 ,
,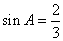 ,则弦
,则弦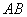 的长为( D )
的长为( D )
A.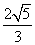 B.
B.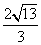 C.4 D.
C.4 D.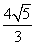
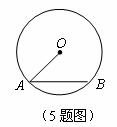
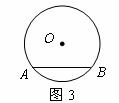
(31)(2008年河北省).如图3,已知 的半径为5,点
的半径为5,点 到弦
到弦 的距离为3,则
的距离为3,则 上到弦
上到弦 所在直线的距离为2的点有( C
)
所在直线的距离为2的点有( C
)
A.1个 B.2个 C.3个 D.4个
(32)(2008山东烟台)如图,水平地面上有一面积为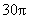 cm2的扇形AOB,半径
cm2的扇形AOB,半径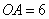 cm,且OA与地面垂直在没有滑动的情况下,将扇形向右滚动至
cm,且OA与地面垂直在没有滑动的情况下,将扇形向右滚动至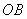 与地面垂直为止,则
与地面垂直为止,则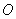 点移动的距离为( C )
点移动的距离为( C )
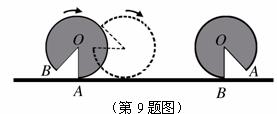
A.20cm B.24cm C.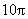 cm D.
cm D.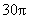 cm
cm
(33)(2008湖北省荆门)如图,将圆沿AB折叠后,圆弧恰好经过圆心,则 (C)等于
(A) 60°. (B) 90°. (C)120°. (D)150°.
(34)(2008年泸州市)如图1,正方形ABCD是⊙O的内接正方形,点P在劣弧 上不同于点C得到任意一点,则∠BPC的度数是( A )
上不同于点C得到任意一点,则∠BPC的度数是( A )
A.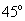 B.
B.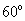 C.
C.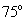 D.
D.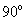
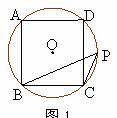
(35)(08长春中考试题)如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16, 那么线段OE的长为( C )
A、10 B、8 C、6 D、4
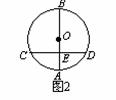
(36)(08长春中考试题)在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是( B )
A.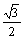 B.1
C.2
D.
B.1
C.2
D. 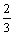
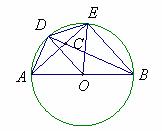
(37)(山东滨州)如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有( D )
A、2个 B、3个 C、4个 D、5个
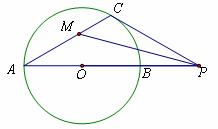
(38)(2008年株洲市)(本题满分7分)如图所示, 的直径AB=4,点P是AB延长线上的一点,过点P作
的直径AB=4,点P是AB延长线上的一点,过点P作 的切线,切点为C,连结AC.
的切线,切点为C,连结AC.
(1)若∠CPA=30°,求PC的长;
(2)若点P在AB的延长线上运动,∠CPA的平分线交AC于点M. 你认为∠CMP的大小是否发生变化?若变化,请说明理由;若化,请求出∠CMP的值.
解:(1)连结OC
由AB=4,得OC=2,在Rt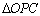 中,
中,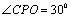 ,得
,得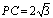
(2)不变 
(39)((08江苏连云港)如图,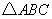 内接于
内接于 ,
,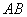 为
为 的直径,
的直径,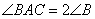 ,
,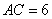 ,过点
,过点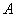 作
作 的切线与
的切线与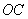 的延长线交于点
的延长线交于点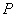 ,求
,求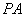 的长.
的长.
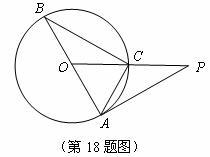
解: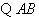 是
是 的直径,
的直径,
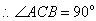 .又
.又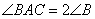 ,
,
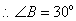 ,
,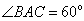
又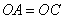 ,所以
,所以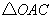 是等边三角形
是等边三角形
由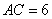 ,知
,知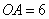 .
.
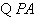 是
是 的切线,
的切线,
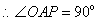 .
.
在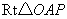 中,
中,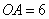 ,
,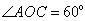 ,
,
所以,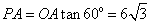
(40)(08江苏连云港)我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段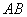 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段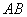 为直径的圆.
为直径的圆.
(1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明);
(3)某地有四个村庄 (其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
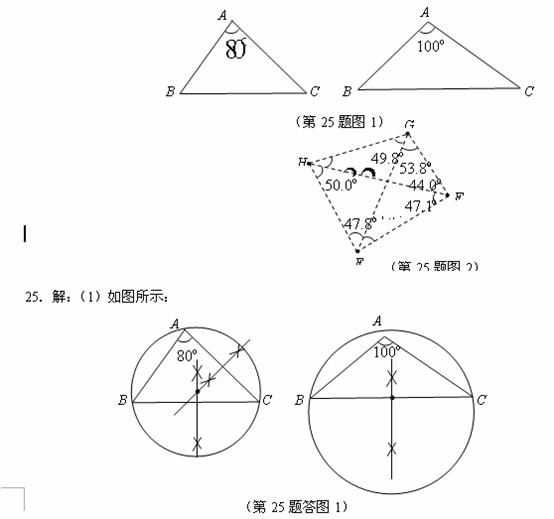
(注:正确画出1个图得2分,无作图痕迹或痕迹不正确不得分)
(2)若三角形为锐角三角形,则其最小覆盖圆为其外接圆;
若三角形为直角或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆.
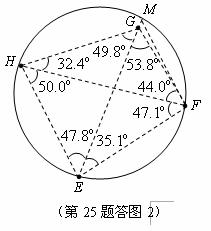
(3)此中转站应建在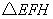 的外接圆圆心处(线段
的外接圆圆心处(线段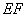 的垂直平分线与线段
的垂直平分线与线段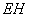 的垂直平分线的交点处).
的垂直平分线的交点处).
理由如下:
由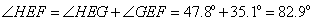 ,
,
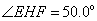 ,
,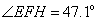 ,
,
故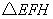 是锐角三角形,
是锐角三角形,
所以其最小覆盖圆为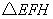 的外接圆,
的外接圆,
设此外接圆为 ,直线
,直线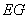 与
与 交于点
交于点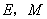 ,
,
则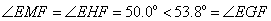 .
.
故点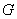 在
在 内,从而
内,从而 也是四边形
也是四边形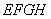 的最小覆盖圆.
的最小覆盖圆.
所以中转站建在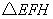 的外接圆圆心处,能够符合题中要求.
的外接圆圆心处,能够符合题中要求.
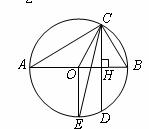
(41)(2008年镇江市)如图,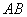 为
为 直径,
直径,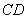 为弦,且
为弦,且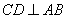 ,垂足为
,垂足为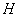 .
.
(1)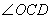 的平分线
的平分线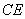 交
交 于
于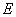 ,连结
,连结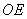 .求证:
.求证: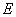 为
为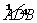 的中点;
的中点;
(2)如果 的半径为
的半径为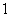 ,
,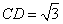 ,
,
①求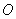 到弦
到弦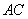 的距离;
的距离;
②填空:此时圆周上存在
个点到直线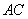 的距离为
的距离为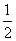 .
.
解:(1)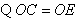 ,
,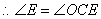
又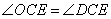 ,
,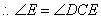
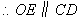
又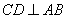 ,
,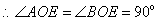 .
.
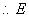 为
为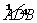 的中点
的中点
(2)①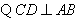 ,
,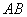 为
为 的直径,
的直径,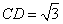 ,
,
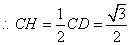
又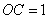 ,
,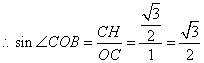
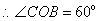
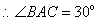 .
.
作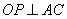 于
于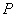 ,则
,则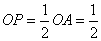
②3
(42)(2008年南通市)已知:如图,M是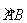 的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=
的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=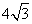 cm.
cm.
(1)求圆心O到弦MN的距离;
(2)求∠ACM的度数.
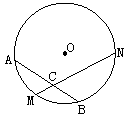
解:(1)连结OM.∵点M是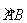 的中点,∴OM⊥AB
的中点,∴OM⊥AB
过点O作OD⊥MN于点D,
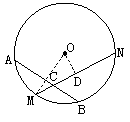
由垂径定理,得MD=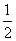 MN=2
MN=2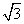 .
.
在Rt△ODM中,OM=4,MD=2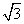 ,∴OD=
,∴OD= =2
=2
故圆心O到弦MN的距离为2cm.
(2)cos∠OMD=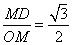 ,
,
∴∠OMD=30°,∴∠ACM=60°
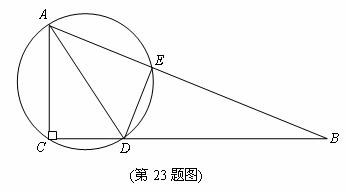
(43)(2008年贵阳市)如图10,已知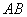 是
是 的直径,点
的直径,点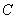 在
在 上,且
上,且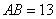 ,
,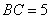 .
.
(1)求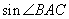 的值.(3分)
的值.(3分)
(2)如果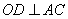 ,垂足为
,垂足为 ,求
,求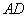 的长.(3分)
的长.(3分)
(3)求图中阴影部分的面积(精确到0.1).(4分)
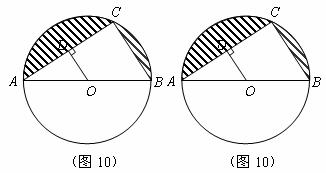
答案:(1)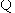 AB是⊙O的直径,点C在⊙O上
AB是⊙O的直径,点C在⊙O上
 ∠ACB = 90o
∠ACB = 90o
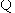 AB=13,BC=5
AB=13,BC=5
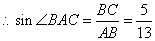 .
.
(2)在Rt△ABC中,
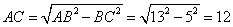 .
.
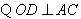 ,
,
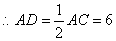 .
.
(3)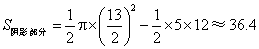 (平方单位)
(平方单位)
点评:(1)问主要考查圆的性质和三角函数的计算;(2)问考查勾股定理的应用和中位线的性质;(3)主要考查圆和三角形面积的计算.
(44)(2008陕西)如图,在 中,
中,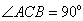 ,
,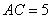 ,
,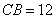 ,
,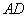 是
是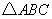 的角平分线.过
的角平分线.过 三点的圆与斜边
三点的圆与斜边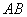 交于点
交于点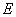 ,连接
,连接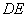 .
.
(1)求证: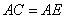 ;
;
(2)求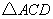 外接圆的半径.
外接圆的半径.
(1)证明: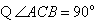 ,
,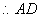 为直径.
为直径.
又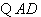 是
是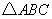 的角平分线,
的角平分线,
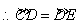 ,
,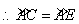 .
.
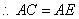 .
.
(2)解: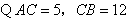 ,
,
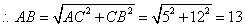 .
.
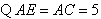 ,
,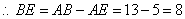 .
.
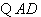 为直径,
为直径,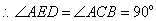 .
.
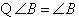 ,
,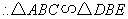 .
.
 .
.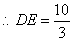 .
.
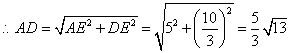 .
.
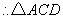 外接圆的半径为
外接圆的半径为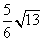 .
.
13.(24)(2008年镇江市)两圆的半径分别为2和3,圆心距为5,则两圆的位置关系为( B )
A.外离 B.外切 C.相交 D.内切
(25)(08河北)如图3,已知 的半径为5,点
的半径为5,点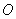 到弦
到弦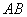 的距离为3,则
的距离为3,则 上
上
到弦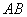 所在直线的距离为2的点有( C )
所在直线的距离为2的点有( C )
A.1个 B.2个 C.3个 D.4个
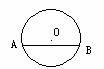
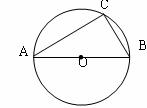
(26)(2008年衢州)如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,则圆心O到弦BC的距离是( B )
A、1.5 B、2 C、2.5 D、3
(27)(2008年衢州)一个圆锥侧面展开图的扇形的弧长为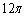 ,则这个圆锥底面圆的半径为( A )
,则这个圆锥底面圆的半径为( A )
A.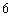 B.
B.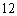
C.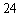 D.
D.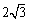
(28)(2008台州)下列命题中,正确的是( C )
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③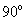 的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等
的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等
A.①②③ B.③④⑤ C.①②⑤ D.②④⑤
(29) (2008年南充市)如图,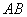 是
是 直径,
直径,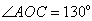 ,则
,则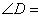 ( B
)
( B
)
A.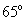 B.
B.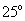 C.
C.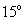 D.
D.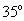
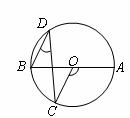
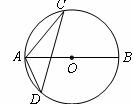
16.(13)(2008湖北黄石)如图,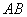 为
为 的直径,点
的直径,点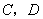 在
在 上,
上,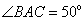 ,则
,则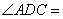 40° .
40° .
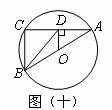
(14)(湖南邵阳)如图(十),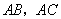 分别是
分别是 的直径和弦,
的直径和弦,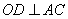 于点
于点 ,连结
,连结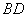 、
、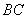 ,
,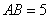 ,
,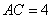 ,则
,则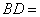
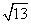 .
.
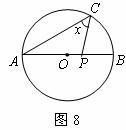
(15)(2008年海南) 如图8, AB是⊙O的直径,点C在⊙O上,∠BAC=30°,点P在线段OB上运动.设∠ACP=x,则x的取值范围是 30°≤x≤90° .
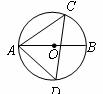
(16)(2008年山西省太原市)如图,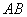 是
是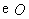 的直径,
的直径,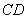 是
是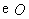 的弦,连接
的弦,连接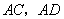 ,
,
若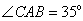 ,则
,则 的度数为 55° .
的度数为 55° .
(17)(2008年辽宁省十二市)16.如图7,直线 与
与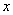 轴、
轴、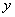 轴分别相交于
轴分别相交于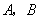
两点,圆心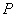 的坐标为
的坐标为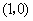 ,
,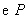 与
与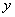 轴相切于点
轴相切于点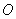 .若将
.若将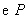 沿
沿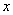 轴向左移动,当
轴向左移动,当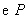 与该直线相交时,横坐标为整数的点
与该直线相交时,横坐标为整数的点
有 3 个.
(18)(2008乌鲁木齐).如图4所示的半圆中, 是直径,且
是直径,且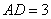 ,
,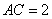 ,
,
则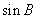 的值是
的值是 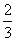 .
.
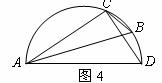
(19)(2008衢州)在半径为5的圆中,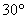 的圆心角所对的弧长为___
的圆心角所对的弧长为___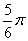 .______
.______
(结果保留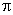 )
)
(20)(2008年衢州)在半径为5的圆中,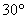 的圆心角所对的弧长为:
的圆心角所对的弧长为: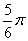 .(结果保留
.(结果保留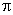 )
)
(21)(2008年佳木斯市)在半径为5cm的圆中,两条平行弦的长度分别为6cm和8cm,则这两条弦之间的距离为 1cm或7cm
(22)(2008乌鲁木齐)如图4所示的半圆中,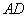 是直径,且
是直径,且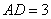 ,
,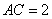 ,
,
则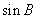 的值是
的值是 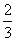 .
.
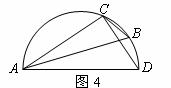
(23)(山东滨州)如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有( D )
A、2个 B、3个 C、4个 D、5个
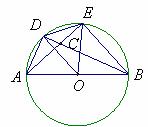
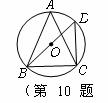
10.(1)(2008年镇江市)如图, 是等腰三角形
是等腰三角形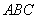 的外接圆,
的外接圆,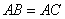 ,
, ,
,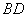 为
为 的直径,
的直径,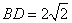 ,连结
,连结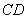 ,则
,则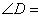 45
45  ,
, 2 .
2 .
(2)(湖南常德)已知⊙ 的半径为5㎝,弦AB的长为8㎝,则圆心
的半径为5㎝,弦AB的长为8㎝,则圆心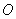 到AB的距离为 3 ㎝.
到AB的距离为 3 ㎝.
(3)(湖南常德)小红量得一个圆锥的母线长为15㎝,底面圆的直径是6㎝,它的侧面积为 45π㎝2(结果保留π).
(4)(2008年江苏省宿迁市)已知直角三角形两条直角边的长是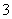 和
和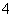 ,则其内切圆的半径是___1___.
,则其内切圆的半径是___1___.
(5)(湖南邵阳)计算机把数据存储在磁盘上,磁盘上有一些同心圆转道.如图(九),现有一张半径为45毫米的磁盘,磁盘的最内磁道半径为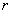 毫米,磁盘的最外圆周不是磁道,磁道上各磁道之间的宽度必须不小于0.3毫米,这张磁盘最多有
毫米,磁盘的最外圆周不是磁道,磁道上各磁道之间的宽度必须不小于0.3毫米,这张磁盘最多有
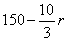 条磁道.
条磁道.
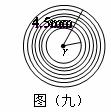
(6)(2008年株洲市)如下图中每个阴影部分是以多边形各顶点为圆心,1为半径的扇形,并且所有多边形的每条边长都大于2,则第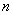 个多边形中,所有扇形面积之和是
(结果保留π).
个多边形中,所有扇形面积之和是
(结果保留π). 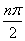

(7)(2008年泸州市)如图8,两个同心圆的半径分别为2和1,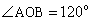 ,则阴影部分的面积为 π
,则阴影部分的面积为 π
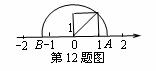
(8)(2008湖北省荆门).如图,半圆的直径AB=__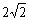 __.
__.
(9)(2008年龙岩市)如图,量角器外沿上有A、B两点,它们的读数分别是70°、40°,
则∠1的度数为 15° .
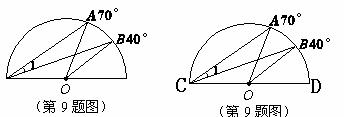
▲
(10)(2008年江苏省迁宿市)已知直角三角形两条直角边的长是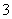 和
和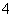 ,则其内切圆的半径是___1___.
,则其内切圆的半径是___1___.
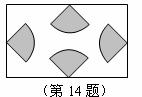
(11)(2008年厦门市)如图,在矩形空地上铺4块扇形草地.若扇形的半径均为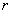 米,圆心角均为
米,圆心角均为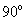 ,则铺上的草地共有
,则铺上的草地共有 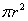 平方米.
平方米.
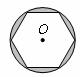
(12)(2008年潍坊市)如图,正六边形内接于圆 ,圆
,圆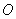 的半径为10,则圆中阴影部分
的半径为10,则圆中阴影部分
的面积为 π-3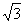 .
.
6. (2008遵义)现有三个多项式: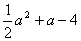 ,
,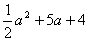 ,
,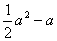 ,请你选择其解:(
,请你选择其解:(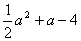 )+(
)+(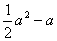 )=
)=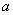 2-4=(
2-4=(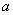 +2)(
+2)(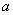 -2)
-2)
中两个进行加法运算,并把结果因式分解。
5. (2008浙江丽水)因式分解: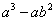 .
.
解:原式=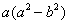 =
=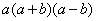
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com