
14、(2008年武汉市)⑴点(0,1)向下平移2个单位后的坐标是
,直线 向下平移2个单位后的解析式是
;
向下平移2个单位后的解析式是
;
⑵直线 向右平移2个单位后的解析式是
;
向右平移2个单位后的解析式是
;
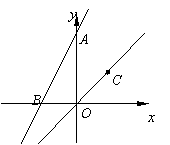
⑶如图,已知点C为直线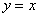 上在第一象限内一点,直线
上在第一象限内一点,直线 交
交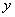 轴于点A,交
轴于点A,交 轴于B,将直线AB沿射线OC方向平移
轴于B,将直线AB沿射线OC方向平移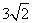 个单位,求平移后的直线的解析式.
个单位,求平移后的直线的解析式.
答案:⑴(0,-1), ;⑵
;⑵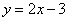 ;⑶
;⑶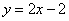 ;
;
12、(2008年北京)如图,已知直线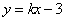 经过点
经过点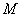 ,求此直线与
,求此直线与 轴,
轴,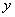 轴的交点坐标.
轴的交点坐标.
解:由图象可知,点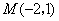 在直线
在直线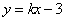 上
上
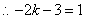 .解得
.解得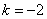 .
.
 直线的解析式为
直线的解析式为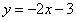 .
.
令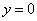 ,可得
,可得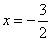 .
.
 直线与
直线与 轴的交点坐标为
轴的交点坐标为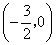 .
.
令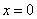 ,可得
,可得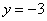 .
.
 直线与
直线与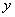 轴的交点坐标为
轴的交点坐标为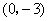 .
.
11、(2008年内江市)如图,一次函数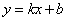 的图象经过第一、二、三象限,且与反比例函数图象相交于
的图象经过第一、二、三象限,且与反比例函数图象相交于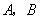 两点,与
两点,与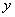 轴交于点
轴交于点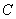 ,与
,与 轴交于点
轴交于点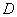 ,
,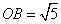 .且点
.且点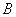 横坐标是点
横坐标是点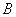 纵坐标的2倍.
纵坐标的2倍.
(1)求反比例函数的解析式;
(2)设点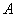 横坐标为
横坐标为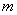 ,
,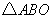 面积为
面积为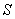 ,
,
求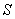 与
与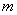 的函数关系式,并求出自变量的取值范围.
的函数关系式,并求出自变量的取值范围.
[解](1)设点B坐标为(2t,t),由题意得
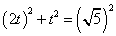 ,解得t = -1
,解得t = -1
故反比例函数的解析式是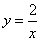 .
.
(2)由一次函数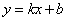 经过
经过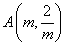 、
、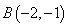 得
得
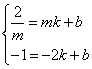 , 解得
, 解得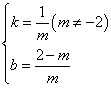 ,
,
所以函数解析式为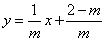
故点D坐标为(m-2,0),
则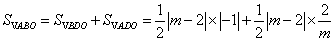
因为b>0,所以有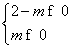 或
或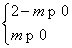 ,
,
解得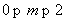 ,
,
故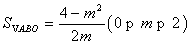
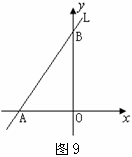
10、(2008梅州)如图所示,直线L与两坐标轴的交点坐标分别是A(-3,0),B(0,4),O是坐标系原点.
(1)求直线L所对应的函数的表达式;
(2)若以O为圆心,半径为R的圆与直线L相切,求R的值.
答案:解:(1)设所求为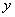 =
=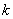
 +
+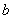 .
.
将A(-3,0),B(0,4)的坐标代入,得
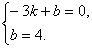
解得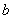 =4,
=4, 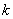 =
=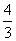 .所求为
.所求为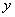 =
=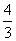
 +4.(2)设切点为P,连OP,则OP⊥AB,OP=R.
+4.(2)设切点为P,连OP,则OP⊥AB,OP=R.
Rt AOB中,OA=3,OB=4,得AB=5,
AOB中,OA=3,OB=4,得AB=5,
因为, 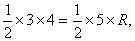 得R=
得R=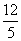 .(本题可用相似三角形求解)
.(本题可用相似三角形求解)
9、(2008年聊城市)已知一次函数与反比例函数的图象交于点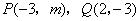 .
.
(1)求这两个函数的函数关系式;
(2)在给定的直角坐标系(如图)中,画出这两个函数的大致图象;
(3)当 为何值时,一次函数的值大于反比例函数的值?当
为何值时,一次函数的值大于反比例函数的值?当 为何值时,一次函数的值小于反比例函数的值?
为何值时,一次函数的值小于反比例函数的值?
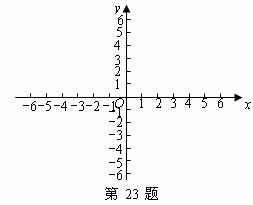
解:(1)设一次函数的关系式为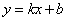 ,反比例函数的关系式为
,反比例函数的关系式为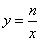 ,
,
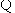 反比例函数的图象经过点
反比例函数的图象经过点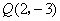 ,
,
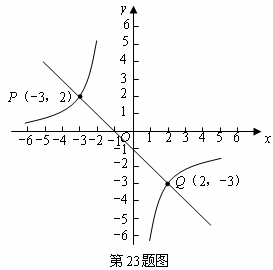
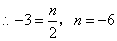 .
.
 所求反比例函数的关系式为
所求反比例函数的关系式为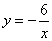 .
.
将点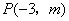 的坐标代入上式得
的坐标代入上式得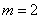 ,
,
 点
点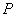 的坐标为
的坐标为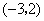 .
.
由于一次函数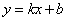 的图象过
的图象过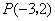 和
和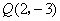 ,
,
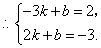 解得
解得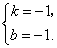
 所求一次函数的关系式为
所求一次函数的关系式为 (2)两个函数的大致图象如图.
(2)两个函数的大致图象如图.
(3)由两个函数的图象可以看出.
当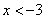 和
和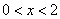 时,一次函数的值大于反比例函数的值.
时,一次函数的值大于反比例函数的值.
当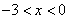 和
和 时,一次函数的值小于反比例函数的值.
时,一次函数的值小于反比例函数的值.
8、(2008年甘肃省兰州市)已知正比例函数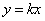 的图象与反比例函数
的图象与反比例函数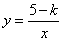 (
(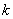 为常数,
为常数,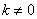 )的图象有一个交点的横坐标是2.
)的图象有一个交点的横坐标是2.
(1)求两个函数图象的交点坐标;
(2)若点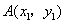 ,
,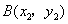 是反比例函数
是反比例函数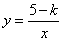 图象上的两点,且
图象上的两点,且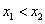 ,试比较
,试比较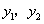 的大小.
的大小.
答案:解:(1)由题意,得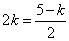 ,解得
,解得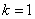 .
.
所以正比例函数的表达式为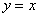 ,反比例函数的表达式为
,反比例函数的表达式为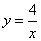 .
.
解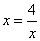 ,得
,得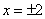 .由
.由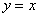 ,得
,得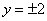 .
.
所以两函数图象交点的坐标为(2,2),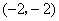 .
.
(2)因为反比例函数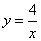 的图象分别在第一、三象限内,
的图象分别在第一、三象限内,
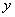 的值随
的值随 值的增大而减小,
值的增大而减小,
所以当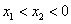 时,
时,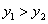 .
.
当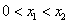 时,
时,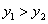 .
.
当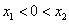 时,因为
时,因为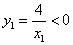 ,
,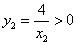 ,所以
,所以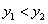 .
.
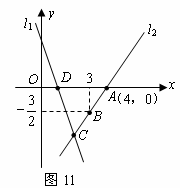
7、[2008年河北省] 如图,直线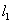 的解析表达式为
的解析表达式为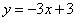 ,且
,且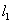 与
与 轴交于点
轴交于点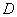 ,直线
,直线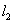 经过点
经过点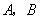 ,直线
,直线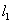 ,
,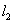 交于点
交于点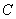 .
.
(1)求点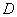 的坐标;
的坐标;
(2)求直线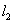 的解析表达式;
的解析表达式;
(3)求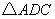 的面积;
的面积;
(4)在直线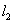 上存在异于点
上存在异于点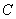 的另一点
的另一点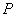 ,使得
,使得
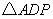 与
与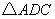 的面积相等,请直接写出点
的面积相等,请直接写出点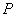 的坐标.
的坐标.
解:(1)由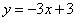 ,令
,令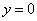 ,得
,得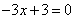 .
.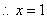 .
.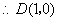 .
.
(2)设直线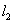 的解析表达式为
的解析表达式为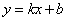 ,由图象知:
,由图象知: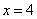 ,
,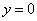 ;
;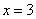 ,
,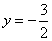 .
.
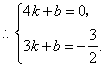
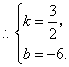
 直线
直线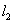 的解析表达式为
的解析表达式为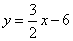 .
.
(3)由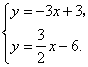 解得
解得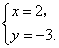
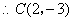 .
.
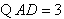 ,
,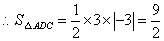 .
.
(4)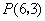 .
.
6、(2008年郴州市)已知一次函数y=ax+b的图像与反比例函数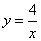 的图像交于A(2,2),B(-1,m),求一次函数的解析式.
的图像交于A(2,2),B(-1,m),求一次函数的解析式.
解:因为B(-1,m)在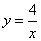 上, 所以
上, 所以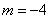
所以点B的坐标为(-1,-4)
又A、B两点在一次函数的图像上,
所以
所以所求的一次函数为y=2x-2
5、(2008年广东省中山市)已知直线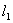 :
: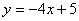 和直线
和直线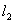 ::
::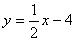 ,求两条直线
,求两条直线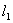 和
和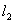 的交点坐标,并判断该交点落在平面直角坐标系的哪一个象限上.
的交点坐标,并判断该交点落在平面直角坐标系的哪一个象限上.
答案解:由题意得,
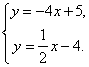
解得,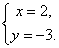 ∴ 直线
∴ 直线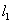 和直线
和直线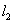 的交点坐标是(2,-3).
的交点坐标是(2,-3).
交点(2,-3)落在平面直角坐标系的第四象限上.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com