
19.(本小题满分7分)
解: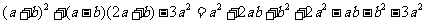 ···················· 3分
···················· 3分
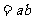 .························································································································· 5分
.························································································································· 5分
当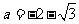 ,
, 时,
时,
原式 ······························································· 7分
······························································· 7分
13. ; 14.110°; 15.
; 14.110°; 15.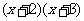 16.18; 17.1; 18.3.
16.18; 17.1; 18.3.
3. 如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.
2. 第三大题(解答题)每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数.部分试题有多种解法,对考生的其他解法,请参考评分意见进行评分.
1. 第一大题(选择题)和第二大题(填空题)的每小题,只有满分和零分两个评分档,不给中间分.
25.(12分)
一次函数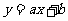 的图象分别与
的图象分别与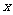 轴、
轴、 轴交于点
轴交于点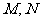 ,与反比例函数
,与反比例函数 的图象相交于点
的图象相交于点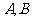 .过点
.过点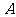 分别作
分别作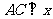 轴,
轴,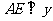 轴,垂足分别为
轴,垂足分别为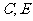 ;过点
;过点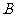 分别作
分别作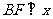 轴,
轴,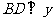 轴,垂足分别为
轴,垂足分别为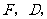
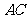 与
与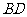 交于点
交于点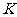 ,连接
,连接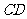 .
.
(1)若点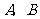 在反比例函数
在反比例函数 的图象的同一分支上,如图1,试证明:
的图象的同一分支上,如图1,试证明:
①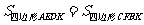 ;
;
②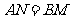 .
.
(2)若点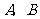 分别在反比例函数
分别在反比例函数 的图象的不同分支上,如图2,则
的图象的不同分支上,如图2,则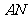 与
与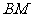 还相等吗?试证明你的结论.
还相等吗?试证明你的结论.
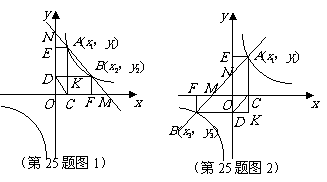
威海市2009年初中升学考试
数学试题参考解答及评分意见
评卷说明:
24.(11分)
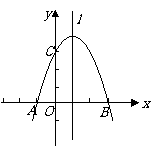 如图,在直角坐标系中,点
如图,在直角坐标系中,点 的坐标分别为
的坐标分别为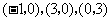 ,过
,过 三点的抛物线的对称轴为直线
三点的抛物线的对称轴为直线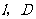 为对称轴
为对称轴 上一动点.
上一动点.
(1) 求抛物线的解析式;
(2)
求当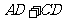 最小时点
最小时点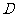 的坐标;
的坐标;
(3)
以点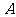 为圆心,以
为圆心,以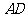 为半径作
为半径作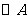 .
.
①证明:当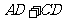 最小时,直线
最小时,直线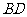 与
与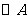 相切.
相切.
②写出直线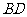 与
与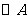 相切时,
相切时, 点的另一个坐标:___________.
点的另一个坐标:___________.
23.(10分)
如图1,在正方形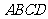 中,
中, 分别为边
分别为边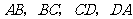 上的点,
上的点, ,连接
,连接 交点为
交点为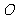 .
.
(1)如图2,连接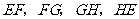 ,试判断四边形
,试判断四边形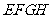 的形状,并证明你的结论;
的形状,并证明你的结论;

(2)将正方形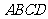 沿线段
沿线段 剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形
剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形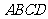 的边长为3cm,
的边长为3cm,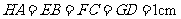 ,则图3中阴影部分的面积为_________
,则图3中阴影部分的面积为_________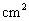 .
.
22.(10分)
响应“家电下乡”的惠农政策,某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台,其中甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超过132 000元.已知甲、乙、丙三种电冰箱的出厂价格分别为:1 200元/台、1 600元/台、2 000元/台.
(1) 至少购进乙种电冰箱多少台?
(2) 若要求甲种电冰箱的台数不超过丙种电冰箱的台数,则有哪些购买方案?
21.(9分)
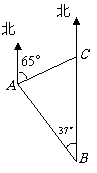
如图,一巡逻艇航行至海面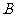 处时,得知其正北方向上
处时,得知其正北方向上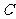 处一渔船发生故障.已知港口
处一渔船发生故障.已知港口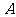 处在
处在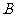 处的北偏西
处的北偏西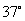 方向上,距
方向上,距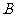 处20海里;
处20海里;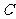 处在A处的北偏东
处在A处的北偏东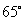 方向上.
方向上.
求 之间的距离(结果精确到0.1海里).
之间的距离(结果精确到0.1海里).
 参考数据:
参考数据:
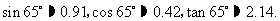
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com