
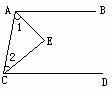
2.如图,EF过△ABC的一个顶点A,且EF∥BC,如果∠B=40°,∠2=75°,那么∠1、∠3、∠C、∠BAC+∠B+∠C各是多少度,为什么?
1.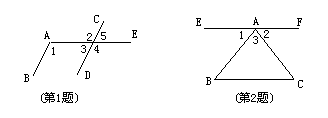 如图,AB∥CD,∠1=102°,求∠2、∠3、∠4、∠5的度数,并说明根据?
如图,AB∥CD,∠1=102°,求∠2、∠3、∠4、∠5的度数,并说明根据?
2.如图所示,已知:∠1=∠2,
求证:∠3+∠4=180°.
分析:(让学生自己分析)
证明:(学生板书)
小结
我们是如何得到平行线的性质定理?通过度量,运用从特殊到一般的思维方式发现性质1(公理),然后由公理通过演绎证明得到后面两个性质定理.从因果关系和所起的作用来看性质定理和判定定理的区别与联系.
作业:
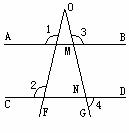
1.如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.
求证:∠1+∠2=90°.
 证明:因为 AB∥CD,
证明:因为 AB∥CD,
所以 ∠BAC+∠ACD=180°,
又因为 AE平分∠BAC,CE平分∠ACD,
所以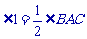 ,
,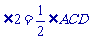 ,
,
 故
故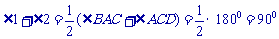 .
.
即 ∠1+∠2=90°.
(理由略)
|
|
|
|
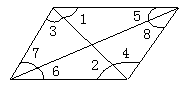
此题一定要强调,哪两条直线被哪一条直线所截.
答:相等的角为:∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8.互补的角为:∠BAC+∠ACD=180°,∠ABD+∠CDB=180°,∠CAB+∠DBA=180°,∠ACD+∠BDC=180°.
相等的角还有:∠ACD=∠ABD,∠BAC=∠BDC.(同角的补角相等)
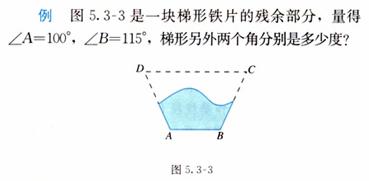
例3如图所示.已知:AD∥BC,∠AEF=∠B,求证:AD∥EF.
分析:(执果索因)从图直观分析,欲证AD∥EF,只需∠A+∠AEF=180°,
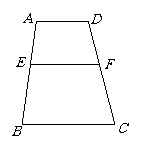 (由因求果)因为AD∥BC,所以∠A+∠B=180°,又∠B=∠AEF,所以∠A+∠AEF=180°成立.于是得证.
(由因求果)因为AD∥BC,所以∠A+∠B=180°,又∠B=∠AEF,所以∠A+∠AEF=180°成立.于是得证.
证明:因为 AD∥BC,(已知)
所以 ∠A+∠B=180°.(两直线平行,同旁内角互补)
因为 ∠AEF=∠B,(已知)
所以 ∠A+∠AEF=180°,(等量代换)
所以 AD∥EF.(同旁内角互补,两条直线平行)
3.平行线判定与性质的区别与联系
投影:将判定与性质各三条全部打出.
(1)性质:根据两条直线平行,去证角的相等或互补.
(2)判定:根据两角相等或互补,去证两条直线平行.
联系是:它们的条件和结论是互逆的,性质与判定要证明的问题是不同的.
2.演绎推理,发现平行线的其它性质
(1)已知:如图,直线AB,CD被直线EF所截,AB∥CD.
求证:∠1= ∠2.
(2)已知:如图2-64,直线AB,CD被直线EF所截,AB∥CD.
求证:∠1+∠2=180°.
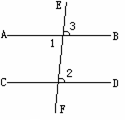
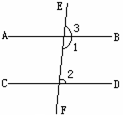
在此基础上指出:“平行线的性质2 (定理)”和“平行线的性质3 (定理)”.
1.实验观察,发现平行线第一个性质
请学生画出下图进行实验观察.
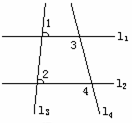
设l1∥l2,l3与它们相交,请度量∠1和∠2的大小,你能发现什么关系?请同学们再作出直线l4,再度量一下∠3和∠4的大小,你还能发现它们有什么关系?
平行线性质1(公理):两直线平行,同位角相等.
2.把它们已知和结论颠倒一下,可得到怎样的语句?它们正确吗?
1.如何用同位角、内错角、同旁内角来判定两条直线是否平行?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com