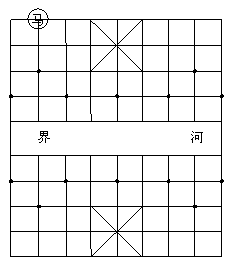
2.如图1所示,B左侧第二个人的位置是 (　 )

　　　 A.(2,5); 　B.(5,2);　 C.(2,2);　 　D.(5,5)

1.如图1所示,一方队正沿箭头所指的方向前进,A的位置为三列四行,表示为(3,4),那么B 的位置是 (　 )毛

　　　 A. (4, 5); B.(5,4);　 C.(4,2); 　D.(4,3)

­　　 如果│3x-13y+16│+│x+3y-2│=0,那么点P(x, y)在第几象限?点Q(x+1,y-1)在坐标平面内的什么位置?

­七、中考题与竞赛题:(共16分)

­　　 如图4所示,图中的能走遍棋盘中的任何一个位置吗?若不能,指出哪些位置无法走到;若能,请说明原因.

­

­　　 如图所示,C,D两点的横坐标分别为2,3,线段CD=1;B,D两点的横坐标分别为-2,3,线段BD=5;A,B两点的横坐标分别为-3,-2,线段AB=1.

­　 (1)如果x轴上有两点M(x₁,0),N(x₂,0)(x₁<x₂),那么线段MN的长为多少?

­　 (2)如果y轴上有两点P(0,y₁),Q(0,y₂)(y₁<y₂),那么线段PQ的长为多少?

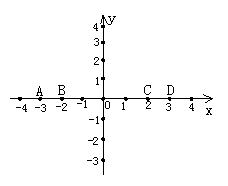
­　 如果点A(t-3s,2t+2s),B(14-2t+s,3t+2s-2)关于x轴对称,求s, t的值.

­　 如果点A的坐标为(a²+1,-1-b²),那么点A在第几象限?为什么?

­1.如图1所示,点A的坐标是 (　 )毛

­　 A.(3,2); ­B.(3,3); C.(3,-3)­;　 D.(-3,-3)

­2.如图1所示,横坐标和纵坐标都是负数的点是 (　 ) A.A点­　　 B.B点　　 ­C.C点­　　 D.D点

­3.如图1所示,坐标是(-2,2)的点是 (　 )

­　 A.点A­ 　　B.点B　　 ­C.点C­ 　　D.点D

­4.若点M的坐标是(a, b),且a>0,b<0,则点M在(　 )

A.第一象限;B.第二象限;­C.第三象限;D.第四象限

­二、填空题:(每小题3分,共15分)

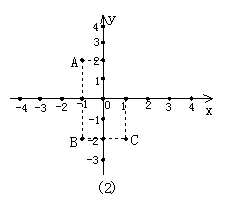
­1.如图2所示,点A的坐标为_______,点A关于x轴的对称点B的坐标为______, 点B关于y轴的对称点C的坐标为________.

­2.在坐标平面内,已知点A(4,-6),那么点A关于x轴的对称点A ′的坐标为_____,点A关于y轴的对称点A″的坐标为_______.

­3.在坐标平面内,已知点A(a, b),那么点A关于x轴的对称点A ′的坐标为______,点A关于y轴的对称点A″的坐标为_____.

­4.点A(-3,2)在第_______象限,点D(-3,-2)在第_______象限,点C( 3, 2) 在第______象限,点D(-3,-2)在第_______象限,点E(0,2)在______轴上, 点F( 2, 0) 在______轴上.

­5.已知点M(a, b),当a>0,b>0时,M在第_______象限;当a____, b______时,M 在第二象限;当a_____, b_______时,M在第四象限;当a<0,b<0时,M在第______象限.

14．(开放题)已知平面直角坐标系中有6个点：

　　 A(3，3)，B(1，1)，C(9，1)，D(5，3)，E(-1，-9)，F(-2，-)．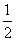

　　 请将上述的6个点分成两类，并写出同类点具有而另一类点不具有的一个特征(特征不能用否定形式表达)．

数学世界

笛卡儿与直角坐标系

　　 笛卡儿(Rene．Descartes)是法国哲学家、数学家、物理学家、解析几何的奠基人之一．

　　 有一次，笛卡儿生病，躺在床上，突然，他看到屋顶上的一只蜘蛛拉着长丝垂下来，灵机一动，他想，可以把蜘蛛看作一个点，它在屋子里上、下、左、右运动，能不能用一组有序的实数，把蜘蛛某一时刻的位置确定下来呢？他又想，屋子里相邻的两面墙，还有地面总共可以交出3条直线，如果把地面上的墙角作为起点，把交出来的3条直线作为3根数轴，那么空间中任何一点的位置，不就可以用在这3根数轴上找到的有序实数来表示吗？

　　 在蜘蛛爬行的启示下，笛卡儿创建了坐标系，坐标系的建立是数学发展的一个重要转折点．

13．(探究题)在直角坐标系中，已知点A(-5，0)，点B(3，0)，△ABC的面积为12，试确定点C的坐标特点．

12．(1)(2005年，福建三明)已知点P₁(a，3)与P₂(-2，-3)关于原点对称，则a=____．

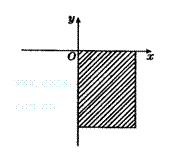　 (2)(2005年，河南)在一次科学探测活动中，探测人员发现一目标在如图所示的阴影区域内，则目标的坐标可能是(　 )

A．(-3，300)　　 B．(7，-500)　 　

C．(9，600)　　 D．(-2，-800)

培优作业