5．三个连续奇数的和是15，那么其中最大的奇数为_______.

4．有一个数，十位数字是a，个位数字是b，十分位数字是c，那么这个数可表示为_______.

3．当k=_______时，方程5x－k=3x+8的解是－2．

2．已知2x+5y＝3，用含y的代数式表示x，则x=___________；当y=1时，x=________

1．若代数式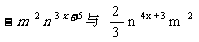是同类项，则x=__________.

11．用作图象的方法解二元一次方程组：(1)将相应的二元一次方程组改写成一次函数的表达式；(2)在同一坐标系内作出这两个一次函数的图象；(3)观察图象的交点坐标，即得二元一次方程组的解．整体相加减求解．利用①+②，得x+y=9③，利用②－①得x－y=3④，可使③、④组成简单的方程组求得x，y．

经典例题剖析：

10．两个一次函数图象的交点与二元一次方程组的解的联系：在同一直 坐标系中，两个一次函数图象的交点的坐标就是相应的二元一次方程组的解．反过来，以二元一次方程组的解为坐标的点一定是相应的两个一次函数的图象的交点，

9．整体思想解方程组．

　 (1)整体代入．如解方程组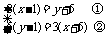，方程①的左边可化为3(x+5)－18=y+5③，把②中的　 3(x+5)看作一个整体代入③中，可简化计算过程，求得y．然后求出方程组的解．

　 (2)整体加减，如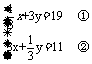因为方程①和②的未知数x、y的系数正好对调，所以可采用两个方程二元一次方程与一次函数的区别和联系．

区别：(1)二元一次方程有两个未知数，而一次函数有两个变量；(2)二元一次方程用一个等式表示两个未知数的关系，而一次函数既可以用一个等式表示两个变量之间的关系，又可以用列表或图象来表示两个变量之间的关系．

　 联系：(1)在直角坐标系中分别描出以二元一次方程的解为坐标的点，这些点都在相应的一次函数的图象上；(2)在一次函数的图象上任取一点，它的坐标都适合相应的二元一次方程．

8．二元一次方程组的解法．

　 (1)代人消元法：解方程组的基本思路是“消元”一把“二元”变为“一元”，主要步骤是，将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来，并代人另一个方程中，从而消去一个未知数，化二元一次方程组为一元一次方程，这种解方程组的方法称为代人消元法，简称代人法．

　 (2)减消无法：通过方程两边分别相加(减)消去其中一个未知数，这种解二元一次方程组的方法叫做加减消元法，简称加减法．

7．二元一次方程组的解：二元一次方程组中各个方程的公共解，叫做这个二元一次方程组的解．