
12、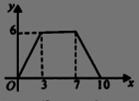 (2007,随州)在四边形
(2007,随州)在四边形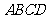 中,
中,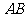 边的长为
边的长为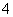 ,设动点
,设动点 沿折线
沿折线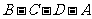 由点
由点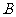 向点
向点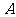 运动,设点
运动,设点 运动的距离为
运动的距离为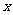 ,
,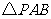 的面积为
的面积为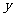 ,
,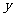 与
与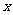 的函数图象如图所示.
的函数图象如图所示.
给出下列四个结论:①四边形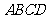 的周和为
的周和为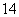 ;②四边形
;②四边形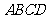 是等腰梯形;③四边形
是等腰梯形;③四边形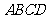 是矩形;④当
是矩形;④当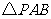 面积为
面积为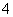 时,点
时,点 移动的距离是
移动的距离是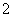 .
.
你认为其中正确的结论是 (只填所有正确结论的序号)
11、(2007,随州)如图,沿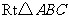 的中位线
的中位线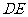 剪切一刀后,用得到的
剪切一刀后,用得到的
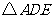 和四边形
和四边形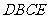 拼图,下列图形中不一定能拼出的是( )
拼图,下列图形中不一定能拼出的是( )
A.平行四边形 B.矩形
C.菱形 D.等腰梯形
10、(2007,宜昌)如图,四边形ABCD是矩形,F是AD上一点,E是CB延长线上一点,且四边形AECF是等腰梯形.下列结论中不一定正确的是( ).
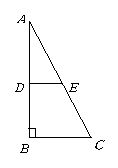
 (A)AE=FC
(B)AD=BC
(A)AE=FC
(B)AD=BC
(C)∠AEB=∠CFD (D)BE=AF
9、(2007,天门)如图,四边形ABCD中,AB∥CD.则下列说法中,不正确的是( ).
A、当AB=CD,AO=DO时,四边形ABCD为矩形
B、当AB=AD,AO=CO时,四边形ABCD为菱形
C、当AD∥BC,AC=BD时,四边形ABCD为正方形
D、当AB≠CD,AC=BD时,四边形ABCD为等腰梯形
8、(2007,湖南)如图,在直角梯形ABCD中,AB//CD,AD⊥CD,AB=1cm,AD=2cm,CD=4cm,则BC= .


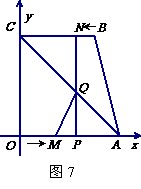
7、(2007,河池)如图7, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点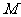 从
从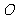 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向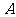 运动;点
运动;点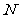 从
从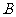 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向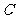 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点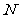 作
作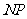 垂直
垂直 轴于点
轴于点 ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ.
(1)点 (填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,说明理由.


6、(2007,河池)已知梯形的两底边长分别为6和8,一腰长为7,则另一腰长a的取值范围是 .
5、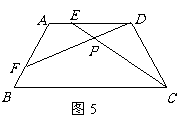 (2007,玉林)如图5,在等腰梯形
(2007,玉林)如图5,在等腰梯形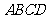 中,
中,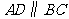 ,
,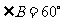 ,
,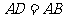 .点
.点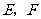 分别在
分别在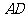 ,
,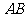 上,
上,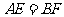 ,
,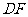 与
与 相交于
相交于 ,则
,则 .
.
4、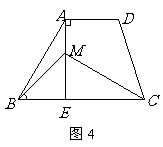 (2007,深圳)如图4,在梯形
(2007,深圳)如图4,在梯形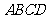 中,
中,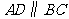 ,
,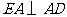 ,
,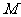 是
是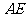 上一点,
上一点,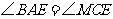 ,
,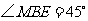 .
.
(1)求证: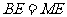 ;(2)若
;(2)若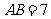 ,求
,求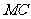 的长.
的长.
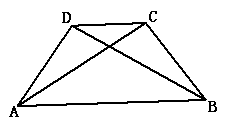
3、(2007,韶山)如图,四边形ABCD中,AD不平行BC,现给出三个条件:①∠CAB=∠DBA,②AC=BD,③AD=BC.请你从上述三个条件中选择两个条件,使得加上这两个条件后能够推出ABCD是等腰梯形,并加以证明(只需证明一种情况).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com