
(Ⅱ)若点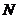 是定直线
是定直线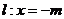 上的任意一点,分别记直线
上的任意一点,分别记直线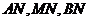 的斜率为
的斜率为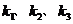 ,试探求
,试探求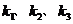 之间的关系,并给出证明.
之间的关系,并给出证明.
(Ⅰ)试证明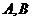 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
 21. (本小题满分15分)过抛物线
21. (本小题满分15分)过抛物线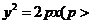
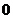
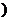 的对称轴上的定点
的对称轴上的定点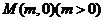 ,作直线
,作直线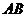 与抛物线相交于
与抛物线相交于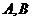 两点.
两点.
(Ⅱ)设PA=k?AB,且二面角E-BD-C的平面角大于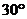 ,求k的取值范围.
,求k的取值范围.
 (Ⅰ)试证:CD
(Ⅰ)试证:CD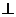 平面BEF;
平面BEF;
20. (本小题满分14分) 如图,在四棱锥P-ABCD中,PA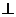 底面ABCD,
底面ABCD,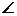 DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
(Ⅰ)求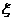 的分布列和期望;
的分布列和期望;
(Ⅱ)若3张卡片是有放回的抽取,则最大号码为4的概率是多少?
19. (本小题满分14分)袋中有6张卡片,编号分别是1,2,3,4,5,6.现在从袋中任意抽取出3张卡片,并记号码最大的为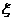 .
.
(Ⅱ)设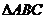 的三边
的三边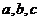 满足
满足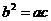 ,且边
,且边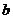 所对应的角为
所对应的角为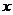 ,若关于
,若关于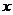 的方程
的方程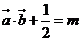 有且仅有一个实数根,求
有且仅有一个实数根,求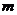 的值.
的值.
(Ⅰ)若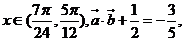 求
求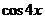 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com