
4.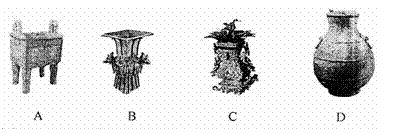 下列青铜器铸造于商代、出土于长江流域的是 ( )
下列青铜器铸造于商代、出土于长江流域的是 ( )
3.在一次国际学术研讨会上,外国学者引用了2300多年前中国思想家的名言:“得道者多
助,失道者寡助。”这位思想家是 ( )
A.老子 B.孔子 C.孟子 D.荀子
2.就论证端午节是中国历史悠久的传统节日而言,下列哪方面的论据应当最有说服力( )
A.古籍的记载 B.屈原的作品 C.政府的声明 D.学者的解释
1.原始人取火困难,保存火和显得非常重要,考古学家发掘出一尊可保存火种的陶制炊具,
推测其最可能出土于 ( )
A.元谋人遗址 B.北京人遗址 C.山顶洞遗址 D.半坡遗址
22、解:
(1)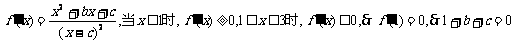
(2) ,其增区间为
,其增区间为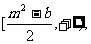 若存在m,则有
若存在m,则有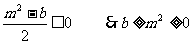 ①
①
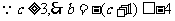 这与①式矛盾,∴不存在实数m.
这与①式矛盾,∴不存在实数m.
21、解:(Ⅰ) 的定义域是
的定义域是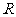 ,
,

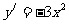
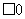 ,
,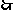
 在
在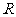 上是单调减函数.
上是单调减函数.
则 在
在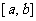 上的值域是
上的值域是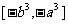 .
.
由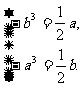 解得:
解得: 或
或 (舍去)或
(舍去)或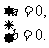 (舍去)
(舍去)
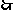 函数
函数 属于集合
属于集合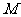 ,且这个区间是
,且这个区间是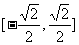 .
.
(Ⅱ)设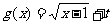 ,则易知
,则易知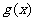 是定义域
是定义域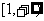 上的增函数.
上的增函数.

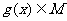 ,
,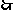 存在区间
存在区间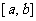
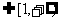 ,满足
,满足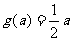 ,
,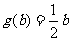 .
.
即方程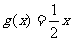 在
在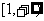 内有两个不等实根.
内有两个不等实根.
[法一]:方程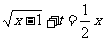 在
在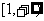 内有两个不等实根,等价于方程
内有两个不等实根,等价于方程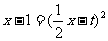 在
在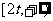 内有两个不等实根.
内有两个不等实根.
即方程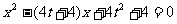 在
在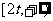 内有两个不等实根.
内有两个不等实根.
根据一元二次方程根的分布有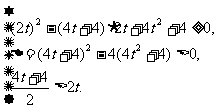
解得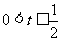 .
.
因此,实数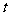 的取值范围是
的取值范围是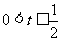 .
.
 [法二]:要使方程
[法二]:要使方程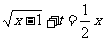 在
在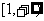 内有两个不等实根,
内有两个不等实根,
即使方程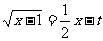 在
在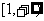 内有两个不等实根.
内有两个不等实根.
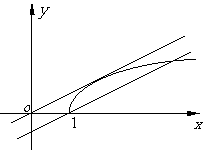
如图,当直线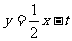 经过点
经过点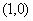 时,
时,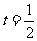 ,
,
当直线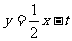 与曲线
与曲线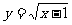 相切时,
相切时,
方程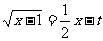 两边平方,得
两边平方,得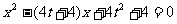 ,由
,由 ,得
,得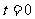 .
.
因此,利用数形结合得实数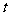 的取值范围是
的取值范围是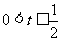 .
.
3]单调递减.
(1)求b、c之间的关系式;
(2)当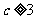 时,是否存在实数m,使得
时,是否存在实数m,使得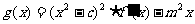 在区间
在区间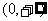 上是单调函数?若存在,求出m的取值范围,若不存在,请说明理由.
上是单调函数?若存在,求出m的取值范围,若不存在,请说明理由.
22、已知函数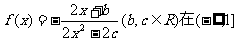 单调递增,在[1,
单调递增,在[1,
21、已知集合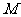 是同时满足下列两个性质的函数
是同时满足下列两个性质的函数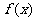 的全体:
的全体:
①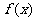 在其定义域上是单调增函数或单调减函数;②在
在其定义域上是单调增函数或单调减函数;②在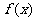 的定义域内存在区间
的定义域内存在区间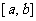 ,使得
,使得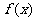 在
在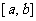 上的值域是
上的值域是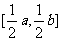 .
.
(Ⅰ)判断函数 是否属于集合
是否属于集合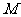 ?并说明理由.若是,请找出区间
?并说明理由.若是,请找出区间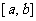 ;
;
((Ⅱ)若函数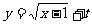
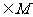 ,求实数
,求实数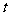 的取值范围.
的取值范围.
20、设函数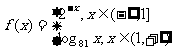 则满足
则满足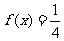 的x值为
的x值为
已知函数是R上的减函数,A(0,-3),B(-2,3)是其图象上的两点,那么不等式的解集是____________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com