
6.四棱锥P-ABCD的底面为正方形,PD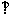 底面ABCD,PD=AD=1.设点C到平面PAB
底面ABCD,PD=AD=1.设点C到平面PAB
的距离为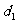 ,点B到平面PAC的距离为
,点B到平面PAC的距离为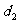 ,则(
)
,则(
)
(A) 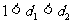 (B)
(B) 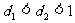
(C) 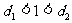 (D)
(D)
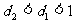
5.正方体AC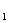 中,E、F分别为AB、CC
中,E、F分别为AB、CC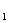 的中点,则异面直线A
的中点,则异面直线A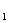 C与EF所成角的余弦值为( )
C与EF所成角的余弦值为( )
(A) 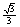 (B)
(B)
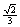
(C) 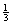 (D)
(D)
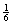
4.对于已知直线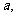 假设直线
假设直线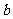 同时满足三个条件:①与
同时满足三个条件:①与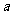 成异面直线;②与
成异面直线;②与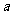 的夹角为定值
的夹角为定值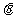 ;③与
;③与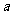 的距离为定值
的距离为定值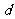 。那么这样的直线
。那么这样的直线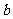 有( )
有( )
(A) 1条 (B) 2条
(C) 4条 (D) 无数条
3.给出以下四个命题:
①
若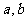 是异面直线,
是异面直线,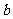 、
、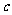 是异面直线,则
是异面直线,则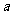 、
、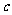 也是异面直线;
也是异面直线;
② 若一条直线与两个平面所成角相等,则这两个平面平行;
③ 若一个二面角的两个面与另一个二面角的两个面分别垂直,则这两个二面角相等或互补;
④ 三个平面两两相交,有三条交线,则三条交线互相平行。
其中正确命题的个数是( )
(A) 0 (B) 1
(C) 2 (D) 3
2.下面有四个命题:
①“直线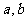 为异面直线”的充分非必要条件是“直线
为异面直线”的充分非必要条件是“直线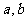 不相交”;
不相交”;
②“直线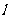
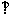 面
面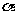 内所有直线”的充要条件是“
内所有直线”的充要条件是“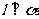 ”;
”;
③“直线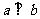 ”的充分非必要条件是“
”的充分非必要条件是“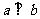 在
在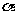 内的射影”;
内的射影”;
④“直线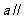 面
面 ”的必要非充分条件是“直线
”的必要非充分条件是“直线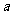 平行于平面
平行于平面 内的一条直线”;
内的一条直线”;
其中正确命题的序号是( )
(A) ①③ (B) ②③
(C) ②④ (D) ②③④
1.正方形纸片ABCD,沿对角线AC对折,使D点在面ABC外,这时DB与面ABC所成的角一定不等于( )
(A) 30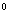 (B) 45
(B) 45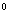
(C) 60 (D) 90
(D) 90
《课课练》 P116-118 课时2中 例题推荐 1、2
课时练习 6、7、8
递推公式 (简单阶差、阶商法)
以上一教时钢管的例子 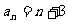
从另一个角度,可以: 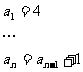
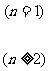
“递推公式”定义:已知数列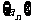 的第一项,且任一项
的第一项,且任一项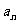 与它的前
与它的前
一项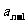 (或前
(或前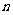 项)间的关系可以用一个公式来表示,这个公式就叫
项)间的关系可以用一个公式来表示,这个公式就叫
做这个数列的递推公式。
例三 (P113 例三)略
例四 已知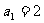 ,
,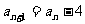 求
求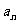 .
.
解一:可以写出: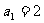 ,
,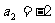 ,
,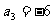 ,
,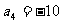 ,……
,……
观察可得:
解二:由题设:
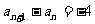
∴ 




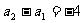

∴ 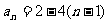
例五 已知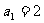 ,
,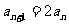 求
求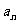 .
.
解一: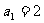
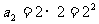
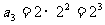
观察可得: 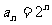
解二:由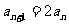 ∴
∴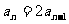 即
即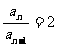
∴ 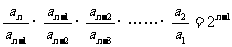
∴ 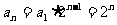
证:显然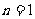 时 ,
时 ,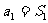
当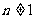 即
即 时
时 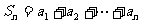
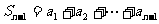
∴ 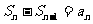 ∴
∴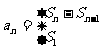
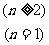
注意:1° 此法可作为常用公式
2° 当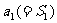 时 满足
时 满足 时,则
时,则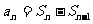
例二:已知数列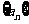 的前n项和为①
的前n项和为① 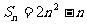 ②
② 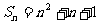
求数列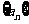 的通项公式。
的通项公式。
解:1.当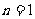 时,
时,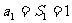
当 时,
时,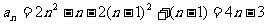
经检验 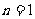 时
时 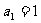 也适合
也适合 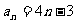
2.当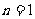 时,
时,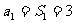
当 时,
时,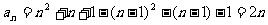
∴ 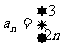
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com