
19.(本题满分14分)
已知函数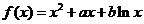 (
( ,实数
,实数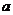 ,
,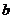 为常数).
为常数).
(Ⅰ)若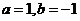 ,求函数
,求函数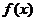 的极值;
的极值;
(Ⅱ)若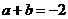 ,讨论函数
,讨论函数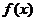 的单调性.
的单调性.
18.(本题满分14分)
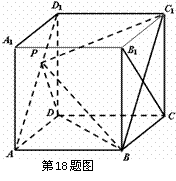 如图,在棱长为
如图,在棱长为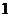 的正方体
的正方体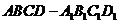 中,
中,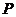 为线段
为线段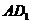 上的点,且满足
上的点,且满足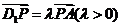 .
.
(Ⅰ)当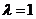 时,求证:平面
时,求证:平面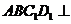 平面
平面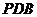 ;
;
(Ⅱ)试证无论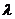 为何值,三棱锥
为何值,三棱锥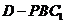 的体积
的体积
恒为定值;
(Ⅲ)求异面直线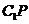 与
与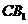 所成的角的余弦值.
所成的角的余弦值.
17.(本题满分12分)
某市为鼓励企业发展“低碳经济”,真正实现“低消耗、高产出”,施行奖惩制度.通过制定评分标准,每年对本市 的企业抽查评估,评出优秀、良好、合格和不合格四个等次,并根据等级给予相应的奖惩(如下表).某企业投入
的企业抽查评估,评出优秀、良好、合格和不合格四个等次,并根据等级给予相应的奖惩(如下表).某企业投入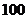 万元改造,由于自身技术原因,能达到以上四个等次的概率分别为
万元改造,由于自身技术原因,能达到以上四个等次的概率分别为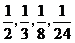 ,且由此增加的产值分别为
,且由此增加的产值分别为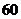 万元、
万元、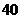 万元、
万元、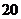 万元、
万元、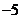 万元.设该企业当年因改造而增加利润为
万元.设该企业当年因改造而增加利润为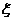 .
.
(Ⅰ)在抽查评估中,该企业能被抽到且被评为合格以上等次的概率是多少?
(Ⅱ)求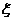 的数学期望.
的数学期望.
16.(本题满分12分)
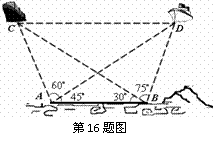 已知海岸边
已知海岸边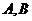 两海事监测站相距
两海事监测站相距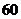
 ,为了测量海平面上两艘油轮
,为了测量海平面上两艘油轮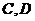 间距离,在
间距离,在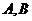 两处分别测得
两处分别测得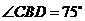 ,
,
 ,
, 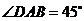 ,
,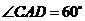
(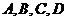 在同一个水平面内).
在同一个水平面内).
请计算出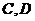 两艘轮船间距离.
两艘轮船间距离.
15.(几何证明选讲)如图,以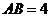 为直径的圆与△ABC的两边
为直径的圆与△ABC的两边
分别交于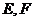 两点,
两点,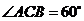 ,则
,则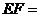 .
.
14.(坐标系与参数方程)极坐标系中,直线 的极坐标方程为
的极坐标方程为
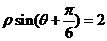 ,则极点在直线
,则极点在直线 上的射影的极坐标是____________.
上的射影的极坐标是____________.
13.若等差数列 的首项为
的首项为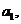 公差为
公差为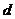 ,前
,前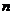 项的和为
项的和为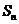 ,则数列
,则数列 为等差数列,且通项为
为等差数列,且通项为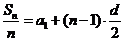 .类似地,若各项均为正数的等比数列
.类似地,若各项均为正数的等比数列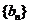 的首项为
的首项为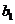 ,公比为
,公比为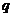 ,前
,前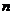 项的积为
项的积为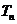 ,则数列
,则数列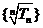 为等比数列,通项为____________________.
为等比数列,通项为____________________.
 (二)选做题(14-15题,考生只能从中选做一题)
(二)选做题(14-15题,考生只能从中选做一题)
12. 若实数 、
、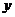 满足
满足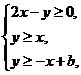 且
且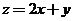 的最小值为
的最小值为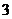 ,则实数
,则实数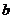 的值为_____.
的值为_____.
11. 右图给出的是计算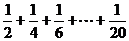 的
的
值的一个框图,其中菱形判断框内应填入的条件是_________.
10. 已知函数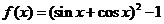 ,
,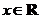 ,
,
则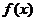 的最小正周期是
.
的最小正周期是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com