
20. 双曲线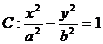 上一点
上一点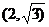 到左,右两焦点距离的差为2.
到左,右两焦点距离的差为2.
(1)求双曲线的方程;
(2)设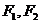 是双曲线的左右焦点,
是双曲线的左右焦点,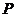 是双曲线上的点,若
是双曲线上的点,若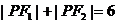 ,
,
求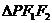 的面积;
的面积;
(3)过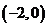 作直线
作直线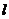 交双曲线
交双曲线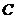 于
于 两点,若
两点,若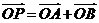 ,是否存在这样的直线
,是否存在这样的直线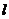 ,使
,使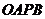 为矩形?若存在,求出
为矩形?若存在,求出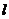 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
18.某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是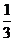 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.
19如图,三棱柱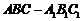 中,侧面
中,侧面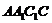
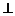 底面
底面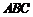 ,
,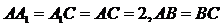 ,且
,且 ,O为
,O为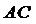 中点.
中点.
(1)证明: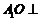 平面
平面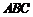 ;
;
(2)求直线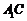 与平面
与平面 所成角的正弦值;
所成角的正弦值;
 (3)在
(3)在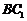 上是否存在一点
上是否存在一点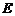 ,使得
,使得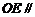 平面
平面 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点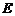 的位置.
的位置.
www.ks%5……
16. 一个袋中有m(m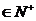 )个红球,3个黑球和2个白球,现从中任取2个球。
)个红球,3个黑球和2个白球,现从中任取2个球。
(1)当m=4时,求取出的2个球颜色相同的概率;
(2)如果取出的2个球颜色不相同的概率小于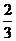 ,求m的最小值。
,求m的最小值。
17 求二项式(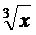 -
-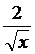 )15的展开式中:
)15的展开式中:
(1)常数项; (2)写出所有的有理项;
15、对于命题:如果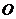 是线段
是线段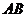 上一点,则
上一点,则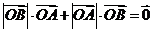 ;将它类比到平面的情形是:若
;将它类比到平面的情形是:若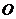 是
是 内一点,有
内一点,有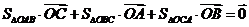 ;将它类比到空间的情形应该是:若
;将它类比到空间的情形应该是:若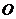 是四面体
是四面体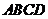 内一点,则有
内一点,则有
____________________________________。
14.把12个相同的小球全部放入4个不同的盒子里,要求每个盒子至少放2个小球,则共有_______________种不同的放法。
13.用数学归纳法证明等式1+2+3+…+(2n+1)=(n+1)(2n+1)时,当n=1左边
所得的项是1+2+3;从“k→k+1”需增添的项是 .
12. 如果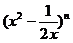 的展开式中只有第4项的二项式系数最大,则展开式中的所有项系数和是
.
的展开式中只有第4项的二项式系数最大,则展开式中的所有项系数和是
.
11. 若复数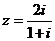 ,则
,则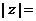
10.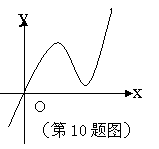 定义在R上的函数
定义在R上的函数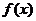 满足
满足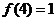 .
.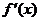 为
为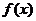 的导函数,已知函数
的导函数,已知函数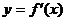 的图象如右图所示.若两正数
的图象如右图所示.若两正数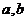 满足
满足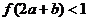 ,则
,则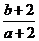 的取值范围是
( )
的取值范围是
( )
A.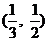 B.
B.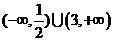
C.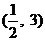 D.
D.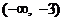
9. 记者要为4名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人
相邻但不排在两端,则不同的排法有 ( )
A.480种 B.72种 C.240种 D. 144种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com