
20.(本小题满分12分)
已知圆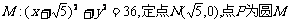 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足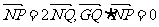 .
.
(I)求点G的轨迹C的方程;
(II)过点(2,0)作直线l,与曲线C交于A、B两点,O是坐标原点,设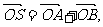 是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
19.(本小题满分12分)
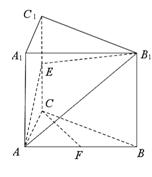 如图,在直三棱柱
如图,在直三棱柱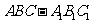 中,
中,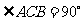 ,
,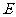 是棱
是棱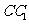 上的动点,
上的动点,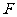 是
是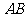 中点 ,
中点 ,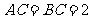 ,
,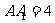 .
.
(Ⅰ)求证: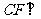 平面
平面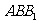 ;
;
(Ⅱ)若二面角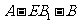 的大小是
的大小是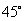 ,求
,求 的长.
的长.
18. (本小题满分12分)
(本小题满分12分)
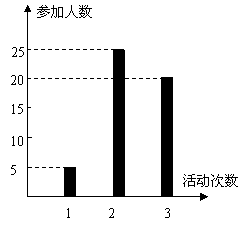
按照新课程的要求, 高中学生在每学期都要至少参
加一次社会实践活动(以下简称活动). 某校高一·
一班50名学生在上学期参加活动的次数统计如条
形图所示.
(I) 求该班学生参加活动的人均次数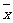 ;
;
(II) 从该班中任意选两名学生,求他们参加活动
次数恰好相等的概率;
(III)从该班中任选两名学生,用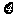 表示这两人参
表示这两人参
加活动次数之差的绝对值,求随机变量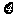 的分布列及数学期望
的分布列及数学期望 .(要求:答案用最简分数表示)学
.(要求:答案用最简分数表示)学
17.(本小题满分12分)在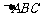 中,
中,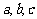 分别为角
分别为角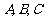 的对边,且满足
的对边,且满足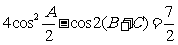
(Ⅰ)求角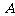 的大小;
的大小;
(Ⅱ)若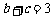 ,求
,求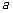 的最小值.
的最小值.
16. 已知函数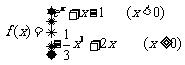 ,给出如下四个命题:
,给出如下四个命题:
①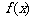 在
在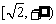 上是减函数;
上是减函数;
②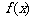 的最大值是2;
的最大值是2;
③函数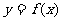 有两个零点;
有两个零点;
④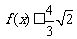 在R上恒成立;
在R上恒成立;
其中正确的命题有 .(把正确的命题序号都填上)
15. 在平面直角坐标系 中,过定点
中,过定点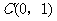 作直线与抛物线
作直线与抛物线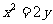 相交于
相交于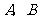 两
两
点.若点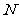 是点
是点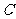 关于坐标原点
关于坐标原点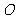 的对称点,则
的对称点,则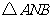 面积的最小值为
.
面积的最小值为
.
14. 已知 ,则
,则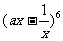 展开式中的常数项为___________.
展开式中的常数项为___________.
13. 为了解某校高中学生的近视眼发病率,在该校学生中进行分层抽样调查,已知该校高一、高二、高三分别有学生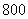 名、
名、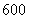 名、
名、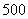 名,若高三学生共抽取
名,若高三学生共抽取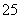 名,则高一年级每一位学生被抽到的概率是___________.
名,则高一年级每一位学生被抽到的概率是___________.
12.已知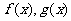 都是定义在R上的函数,
都是定义在R上的函数,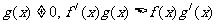 ,且
,且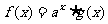
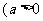 ,且
,且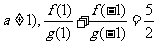 .若数列
.若数列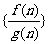 的前n项和大于62,则n的最小值为( )
的前n项和大于62,则n的最小值为( )
(A)6 (B)7 (C)8 (D)9
第Ⅱ卷
本卷包括必考题和选考题两部分。第(13)题-第(21)题为必考题,每个试题考生都必须作答。第(22)题-第(24)题为选考题,考生根据要求作答。
11.在三棱柱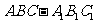 中,各棱长相等,侧棱垂直于底面,点
中,各棱长相等,侧棱垂直于底面,点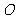 是侧面
是侧面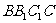 的中心,点
的中心,点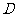 为平面
为平面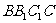 内一点,若
内一点,若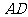 与平面
与平面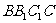 所成的角为
所成的角为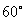 ,则点
,则点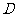 可能在下列哪些位置( )
可能在下列哪些位置( )
(A)点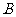 和
和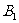 处
(B)点
处
(B)点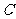 和
和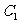 处
处
(C)点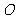 ,
,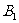 和
和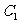 处
(D)来.网点
处
(D)来.网点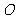 ,
,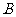 和
和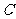 处
处
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com