
9、若关于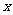 的不等式组
的不等式组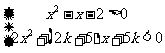 的整数解集
的整数解集
为 ,则实数
,则实数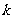 的取值范围是
的取值范围是
8、在棱长为1的正四面体ABCD中,E是BC的中点,
则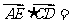 .
.
7、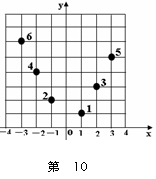 已知正数
已知正数 、
、 满足
满足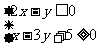 ,则
,则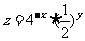 的最小值为 .
的最小值为 .
6、设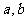 为互不相等的正整数,方程
为互不相等的正整数,方程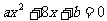 的两个实根为
的两个实根为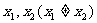 ,且
,且 ,则
,则 的最小值为 .
的最小值为 .
5、已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的 判断框内①处应填 .
4、抛物线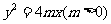 的焦点到双曲线-=l的一条渐近线的距离为3,则此抛物线的准线方程为
.
的焦点到双曲线-=l的一条渐近线的距离为3,则此抛物线的准线方程为
.
3、 命题:“
命题:“ ”的否定是
.
”的否定是
.
2.、已知 中,
中,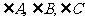 的对边分别为
的对边分别为 若
若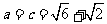 ,且
,且
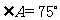 ,则
,则 .
.
1、已知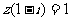 ,则复数
,则复数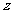 在复平面上对应的点位于第 象限.
在复平面上对应的点位于第 象限.
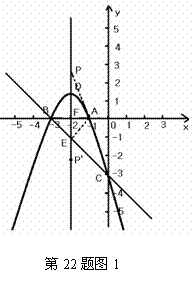
25、⑴∵抛物线 经过A(-1,0),B(-3,0),
经过A(-1,0),B(-3,0),
∴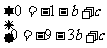
 解得:
解得:
∴抛物线的解析式为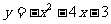 .
.
⑵ 由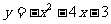 .
.
可得D(-2,1),C(0,-3).
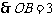 ,
,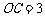 ,
,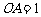 ,
, .
.
可得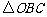 是等腰直角三角形.
是等腰直角三角形.
 ,
, .
.
如图1,设抛物线对称轴与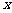 轴交于点
轴交于点 ,
,
 .
.
过点 作
作 于点
于点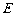 .
.
|
 .
.
可得 ,
, .
.
在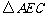 与
与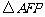 中,
中,
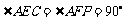 ,
, ,
,
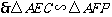 .
.
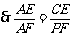 ,
, .
.
解得 .
.
 点
点 在抛物线的对称轴上,
在抛物线的对称轴上,
 点
点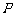 的坐标为(-2,2)或(-2,-2).
的坐标为(-2,2)或(-2,-2).
(3)设直线BC的解析式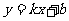 ,
,
直线BC经过B(-3,0),C(0,-3),
∴
解得:k=-1,b=-3,
∴直线BC的解析式
设点Q(m,n),过点Q作QH⊥BC于H,并过点Q作QS∥y轴交直线BC于点S,则S点坐标为(m,-m-3)
∴QS=n-(-m-3)=n+m+3. ------------------11分
∵点Q(m,n)在抛物线y=-x2-4x-3上,
∴n=-m2-4m-3.
∴QS=-m2-4m-3+m+3
=-m2-3m
=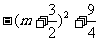
当m= 时,QS有最大值
时,QS有最大值 .
.
∵BO=OC,∠BOC=90°,
∴∠OCB=45°.
∵QS∥y轴,
∴∠QSH=45°.
∴△QHS是等腰直角三角形.
∴当斜边QS最大时QH最大.
∵当m= 时,QS最大,
时,QS最大,
∴此时n=-m2-4m-3=- +6-3=
+6-3= .
.
∴Q(-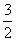 ,
, )
)
∴Q点的坐标为(-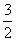 ,
, )时,点Q到直线BC的距离最远。
)时,点Q到直线BC的距离最远。
(注:① 如果学生有不同的解题方法,只要正确,可参考评分标准,酌情给分;
② 对第(3)题,如果只用△=0求解,扣2分。理由:△=0判断只有一个交点,不是充分条件)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com