
9、在研究身高和体重的关系时,求得相关指数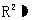 ______________,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
______________,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
8、变量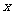 与
与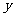 具有线性相关关系,当
具有线性相关关系,当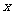 取值16,14,12,8时,通过观测得到
取值16,14,12,8时,通过观测得到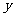 的值分别为11,9,8,5,若在实际问题中,
的值分别为11,9,8,5,若在实际问题中,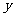 的预报最大取值是10,则
的预报最大取值是10,则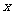 的最大取值不能超过(
)
的最大取值不能超过(
)
(A)16 (B)17 (C)15 (D)12
7、考察棉花种子经过处理跟生病之间的关系得到如下表数据:
|
|
种子处理 |
种子未处理 |
合计 |
|
得病 |
32 |
101 |
133 |
|
不得病 |
61 |
213 |
274 |
|
合计 |
93 |
314 |
407 |
根据以上数据,则( )
(A)种子经过处理跟是否生病有关 (B)种子经过处理跟是否生病无关
(C)种子是否经过处理决定是否生病 (D)以上都是错误的
6、为研究变量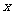 和
和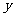 的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程
的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程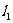 和
和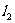 ,两人计算知
,两人计算知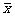 相同,
相同,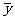 也相同,下列正确的是( )
也相同,下列正确的是( )
(A) 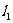 与
与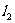 重合
(B)
重合
(B) 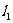 与
与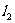 一定平行
一定平行
(C) 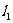 与
与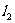 相交于点
相交于点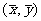 (D) 无法判断
(D) 无法判断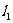 和
和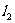 是否相交
是否相交
5、工人月工资(元)依劳动生产率(千元)变化的回归直线方程为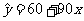 ,下列判断正确的是( )
,下列判断正确的是( )
(A)劳动生产率为1000元时,工资为50元
(B)劳动生产率提高1000元时,工资提高150元
(C)劳动生产率提高1000元时,工资提高90元
(D)劳动生产率为1000元时,工资为90元
4、两个变量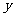 与
与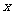 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数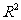 如下
,其中拟合效果最好的模型是( )
如下
,其中拟合效果最好的模型是( )
(A)模型1的相关指数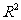 为0.98 (B) 模型2的相关指数
为0.98 (B) 模型2的相关指数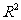 为0.80
为0.80
(C)模型3的相关指数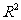 为0.50 (D) 模型4的相关指数
为0.50 (D) 模型4的相关指数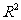 为0.25
为0.25
3、一位母亲记录了儿子3-9岁的身高,由此建立的身高与年龄的回归模型为y=7.19x+73.93
用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
(A)身高一定是145.83cm (B)身高在145.83cm以上
(C)身高在145.83cm以下 (D)身高在145.83cm左右
2、设两个变量x和y之间具有线性相关关系,它们的相关系数是r,y关于x的回归直线的斜率是b,纵截距是a,那么必有( )
(A) b与r的符号相同 (B) a与r的符号相同
(C) b与r的相反 (D) a与r的符号相反
12.已知10只狗的血球体积及红血球的测量值如下(x(血球体积,mm),y(血红球数,百万)):
|
x |
45 |
42 |
46 |
48 |
42 |
35 |
58 |
40 |
39 |
50 |
|
y |
6.53 |
6.30 |
9.25 |
7.50 |
6.99 |
5.90 |
9.49 |
6.20 |
6.55 |
7.72 |
(1)画出上表的散点图; (2)求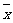 ,
,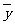 ,
,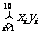 ,
,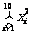 ;
(3)由散点图判断能否用线性回归方程来刻画
;
(3)由散点图判断能否用线性回归方程来刻画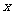 与
与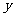 之间的关系,若能,求出线性回归方程.
之间的关系,若能,求出线性回归方程.
 选修1-2
第1章
统计案例
选修1-2
第1章
统计案例
§1.3统计案例单元测试
参考公式
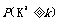 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
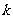 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
在画两个变量的散点图时,下面哪个叙述是正确的( )
(A)预报变量在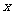 轴上,解释变量在
轴上,解释变量在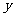 轴上
轴上
(B)解释变量在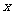 轴上,预报变量在
轴上,预报变量在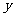 轴上
轴上
(C)可以选择两个变量中任意一个变量在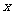 轴上
轴上
(D)可以选择两个变量中任意一个变量在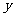 轴上
轴上
11.在某年一项关于16艘轮船的研究中,船的吨位区间从192吨到3246吨,船员的数目从5人到32人.船员人数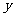 关于船的吨位
关于船的吨位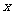 的线性回归方程为
的线性回归方程为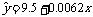
(1)假设两艘轮船吨位相差1000吨,则船员平均人数相差多少?
(2)对于最小的船估计的船员数是多少?对于最大的船估计的船员数是多少?(本小题保留整数)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com