
2.代表银川的序号是 ( )
A.① B.② C.③ D.④
22.(本小题满分14分)
已知函数 。
。
(Ⅰ)若函数 在区间
在区间 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若 是函数
是函数 的极值点,求函数
的极值点,求函数 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)在(Ⅱ)的条件下,是否存在实数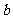 ,使得函数
,使得函数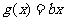 的图象与函数
的图象与函数 的
的
图象恰有3个交点?若存在,请求出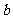 的取值范围;若不存在,试说明理由。
的取值范围;若不存在,试说明理由。
21.(本小题满分12分)
椭圆 与直线
与直线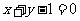 相交于
相交于 、
、 两点,且
两点,且 (
(
为坐标原点).
(Ⅰ)求证: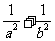 等于定值;
等于定值;
(Ⅱ)当椭圆的离心率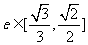 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围.
20.(本小题满分12分)
设同时满足条件:① ;②
;②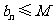 (n∈N*,M是与
(n∈N*,M是与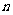 无关的常
无关的常
数)的无穷数列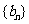 叫“特界”数列。
叫“特界”数列。
(Ⅰ)若数列 为等差数列,
为等差数列, 是其前
是其前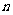 项和,
项和, ,求
,求 ;
;
(Ⅱ)判断(Ⅰ)中的数列 是否为“特界”
数列,并说明理由。
是否为“特界”
数列,并说明理由。
19.(本小题满分12分)
如图,四边形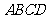 为矩形,
为矩形, 平面
平面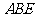 ,
,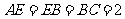 ,
,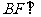 平面
平面
于点 ,且点
,且点 在
在 上。
上。
 (Ⅰ)求证:
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥 的体积;
的体积;
(Ⅲ)设点 在线段
在线段 上,且满足
上,且满足 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得
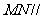 平面
平面 。
。
18.(本小题满分12分)
已知关于 的一元二次方程
的一元二次方程 .
.
(Ⅰ)若 是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(Ⅱ)若 ,求方程没有实根的概率.
,求方程没有实根的概率.
17.(本小题满分12分)
在 中,
中,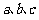 分别为角
分别为角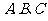 的对边,且满足
的对边,且满足 .
.
(Ⅰ)求角 的值;
的值;
(Ⅱ)若 ,设角
,设角 的大小为
的大小为
 的周长为
的周长为 ,求
,求 的最大值.
的最大值.
16.已知双曲线 的左、右焦点分别为F1、
的左、右焦点分别为F1、
F2, 是双曲线上的一点,若
是双曲线上的一点,若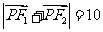 ,
,
则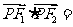 。
。
15. 已知数列2008,2009,1,-2008,-2009,
已知数列2008,2009,1,-2008,-2009,
……这个数列的特点是从第二项起,每一项都
等于它的前后两项之和,则这个数列的前2009
项之和 等于
。
等于
。
14.如果执行如图所示的程序,那么输出的值 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com