9. 在极坐标系中，圆的圆心的极坐标是________，它与方程所表示图形的交点的极坐标是____________.　

8.如图所示的三角形数阵叫“莱布尼兹调和三角形”，它是由整数的倒数组成的，第行有

个数，且两端的数均为，每个数是它下一行左右相邻两数的和，如：

，，则第行的第个数(从左至右数)

为(　　 )　　　　　　　　　　　　　　　　　　　　　　　　　

A.　　 　　 B.　 　　　 C. 　 　　　D. 　

7. 已知实数满足，如果目标函数的最小值为，则实数等于(　 )

A. 　　　　B. 　 　　　　　 C.　 　　　　　 　　D. 　　

6. 如图：内接于，，直线切于点，交于

点，若，则的长为(　 )

　　 A. 　　　　　　 B. 　　　　　　 C.　 　　　 　　D.

5.从甲、乙等名同学中挑选名同学参加某项公益活动，要求 甲、乙至少有一人参加，则不同的挑选方法共有(　　 )　　　　　　　

A. 种　　　 B.　 种　　　　 　 C. 种 　　　 D. 种

4.已知函数的图像与直线的两个相邻交点的距离等于，则的单调递增区间是(　　 )　　　　　　　　　　　　　　　　　　　　

A.　 　　B. 　　

C.　 　　　D.

3.已知函数，则的值是(　　 )

　　 A.　　　 B. 　　　C. 　　　D. 　　　　　　　　　　　　　　　　　　　　　　　　　　

2.已知是实数，若是虚数单位，且为纯虚数，则的值是(　　 )

A. 　　　　B. 1　　 C．　　　　　 D. 　

1.已知：直线与平面内无数条直线垂直，：直线与平面垂直，则是的(　 )

A. 充分不必要条件　　　　　　 B. 必要不充分条件　

C．充要条件　　　　　　　　　 D. 既不充分也不必要条件　　

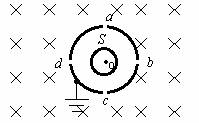[例6]如图所示，两个共轴的圆筒形金属电极，外电极接地，其上均匀分布着平行于轴线的四条狭缝a、b、c和d，外筒的外半径为r，在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场，磁感强度的大小为B。在两极间加上电压，使两圆筒之间的区域内有沿半径向外的电场。一质量为m、带电量为+q的粒子，从紧靠内筒且正对狭缝a的S点出发，初速为零。如果该粒子经过一段时间的运动之后恰好又回到出发点S，则两电极之间的电压U应是多少？(不计重力，整个装置在真空中)

解析：如图所示，带电粒子从S点出发，在两筒之间的电场作用下加速，沿径向穿过狭缝a而进入磁场区，在洛伦兹力作用下做匀速圆周运动。粒子再回到S点的条件是能沿径向穿过狭缝d.只要穿过了d，粒子就会在电场力作用下先减速，再反向加速，经d重新进入磁场区，然后粒子以同样方式经过c、b，再回到S点。设粒子进入磁场区的速度大小为V，根据动能定理，有

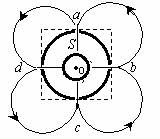
设粒子做匀速圆周运动的半径为R，由洛伦兹力公式和牛顿第二定律，有

由前面分析可知，要回到S点，粒子从a到d必经过圆周，所以半径R必定等于筒的外半径r，即R=r.由以上各式解得；

.

[例7]如图所示，空间分布着有理想边界的匀强电场和匀强磁场。左侧匀强电场的场强大小为E、方向水平向右，电场宽度为L；中间区域匀强磁场的磁感应强度大小为B，方向垂直纸面向里。一个质量为m、电量为q、不计重力的带正电的粒子从电场的左边缘的O点由静止开始运动，穿过中间磁场区域进入右侧磁场区域后，又回到O点，然后重复上述运动过程。求：

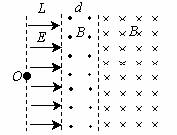
(1)中间磁场区域的宽度d；

(2)带电粒子从O点开始运动到第一次回到O点所用时间t.

解析：(1)带电粒子在电场中加速，由动能定理，可得：　

带电粒子在磁场中偏转，由牛顿第二定律，可得：

由以上两式，可得。

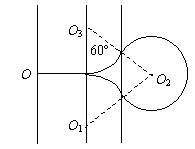
可见在两磁场区粒子运动半径相同，如图13所示，三段圆弧的圆心组成的三角形ΔO₁O₂O₃是等边三角形，其边长为2R。所以中间磁场区域的宽度为

(2)在电场中

，

在中间磁场中运动时间

在右侧磁场中运动时间，

则粒子第一次回到O点的所用时间为

。