
65.解析:这是一道细节推断题。从广告I的第二段“Viewing is available on a first-come-first-served basis”可知观看比赛的原则是先来先服务。因此,来得早的观众能得到好的观看位置。
64.解析: 这是一道推断题。从广告I第一段“the historic 12-minute all-you-can-eat competition will begin.”可知,这是一场吃的比赛。
67. From the advertisement we know that Frojel used to be ______.
A. a Viking club. B. a family-based society
C. a European island D. a trading center
答案 64.B 65.A 66.D 67.D
66. The best title for Advertisement 2 would be _______.
A. The Vikings B. Reliving of the Vikings
C Frojel D. A Viking Reliving Society
65. People who come to watch the competition earliest may _______.
A. get the best watching position B. get the best food.
C. watch whatever they want to D. take good pictures
64. According to AdvertisementⅠ, the famous yearly competition is ______.
A. a music competition B. an eating competition
C. a cooking competition D. a pleasure-taking competition
17. 本题主要考查概率、统计等基础知识,考查数据处理能力、运算求解能力,考查分类与整
合思想、化归与转化思想.
解:(Ⅰ)∵3名工人选择的项目均为A 类工程的概率
类工程的概率 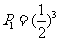 ,……………………(1分)
,……………………(1分)
均为B类工程的概率 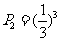 ,
…………………
,
………………… ……(2分)
……(2分)
均为C类工程的概率 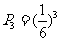 ,
………………………(3分)
,
………………………(3分)
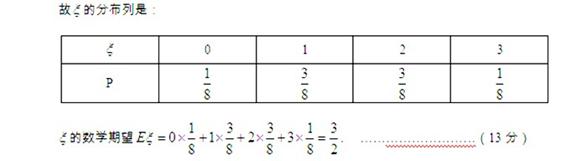
∴他们选择的项目所属工程类别相同的概率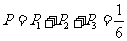 . …………(5分)
. …………(5分)
(Ⅱ)设三名工人中选择项目属于A类工程的人数为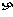 ,则
,则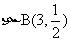 ,
,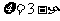 .
.
………………………(7分)
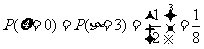 , ………………………(8分)
, ………………………(8分)
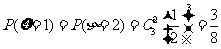 , ………………………(9分)
, ………………………(9分)
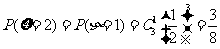 , ………………………(10分)
, ………………………(10分)
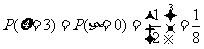 . ………………………(11分)
. ………………………(11分)
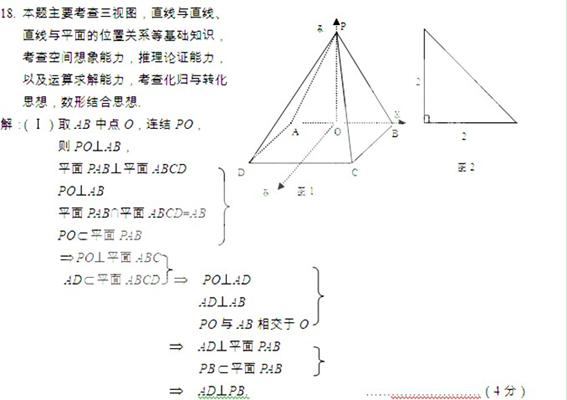 (Ⅱ)过O作AD的平行线为x轴,OB、OP分别为y、z轴,建立空间直角坐标系,则
(Ⅱ)过O作AD的平行线为x轴,OB、OP分别为y、z轴,建立空间直角坐标系,则


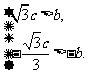 ………………………(6分)
………………………(6分)
即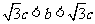 ,∴
,∴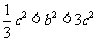 ,∴
,∴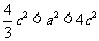 .
.
故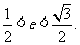 ………………………(8分)
………………………(8分)
(3)直线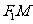 与直线
与直线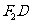 的交点在定直线
的交点在定直线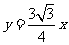 上, ………………………(9分)
上, ………………………(9分)
证明如下:由(1)有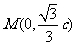 ,因为A、B、M、O、C六点均匀分布,则必有
,因为A、B、M、O、C六点均匀分布,则必有


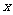 |
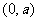 |
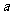 |
 |
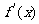 |
+ |
0 |
- |
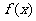 |
↗ |
|
↘ |
故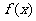 在
在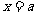 处取得极大值.
处取得极大值.
要使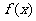 在区间
在区间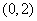 上无极值,则
上无极值,则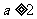 .
.
综上所述,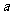 的取值范围是
的取值范围是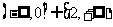 .
………………………(9分)
.
………………………(9分)
(Ⅲ)由(Ⅱ) 知,当
知,当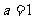 时,
时,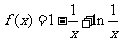 在
在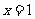 处取得最大值
处取得最大值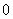 .
.
即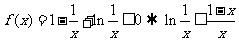 .
.
令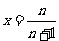 ,则
,则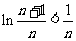 ,即
,即 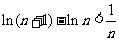 ,
,
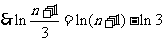


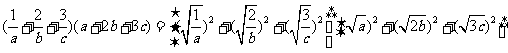
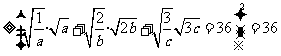 .
………………………(5分)
.
………………………(5分)
又 ,
,  . 当且仅当
. 当且仅当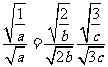 ,
,
即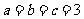 时等式成立.
时等式成立.
∴当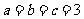 时,
时,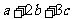 取得最小值18. ………………………(7分)
取得最小值18. ………………………(7分)

21. 本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题做答,满分14 分,如果多做,则按所做的前两题计分. 作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中
分,如果多做,则按所做的前两题计分. 作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中
(Ⅰ)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵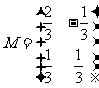 ,
, 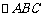 的顶点为A(0,0),B(2,0),C(1,2),求
的顶点为A(0,0),B(2,0),C(1,2),求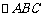
在矩阵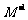 的变换作用下所得
的变换作用下所得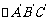 的面积.
的面积.
(Ⅱ)(本小题满分7分)选修4-4:坐标系与参数方程
极坐标的极点是直角坐标系原点,极轴为X轴正半轴,直线l的参数方程为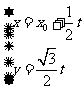
(t为参数)。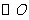 的极坐标方程为
的极坐标方程为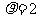 ,若直线l与
,若直线l与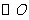 相切,求实数
相切,求实数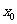 的值。
的值。
(Ⅲ)(本小题满分7分)选修4-5:不等式选讲
已知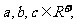 且
且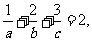 求
求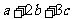 的最小值及取得最小值时
的最小值及取得最小值时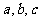 的值。
的值。

 ∴
∴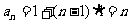 .
………………………(5分)
.
………………………(5分)
(2)由(1)得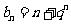
若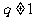 ,则
,则 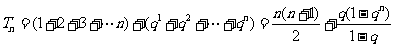
………………………(9分)
若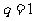 则
则
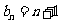 ,
, 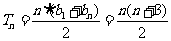 ………………………(13分
………………………(13分 )
)
20. (本题满分14分)
已知函数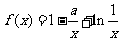 (
(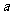 为实常数)。
为实常数)。
(Ⅰ)当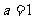 时,求函数
时,求函数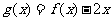 的单调区间;
的单调区间;
(Ⅱ)若函数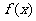 在区间
在区间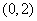 上无极值,求
上无极值,求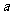 的取值范围;
的取值范围;
(Ⅲ)已知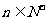 且
且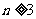 ,求证:
,求证: 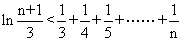 .
.
19. (本题满分 13分)
13分)
平面直角坐标系xOy中,已知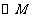 经过点
经过点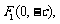

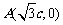 三点,其中
三点,其中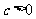 .
.
(Ⅰ)求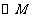 的标准方程(用含
的标准方程(用含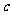 的式子表示);
的式子表示);
(Ⅱ)已知椭圆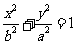 (其中
(其中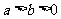 ,
,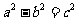 )的左、右顶点分别为D、
)的左、右顶点分别为D、
B,
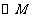 与X轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧,
与X轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧,
求椭圆离心率的取值范围;
(Ⅲ)若A、B、M、O、C、D(O为坐标原点)依次均匀分布在X轴上,问直线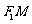 与直线
与直线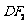 的交点是否在一条定直线上?如果是,请求出这条定直线的方程,如果不是,请说明理由
的交点是否在一条定直线上?如果是,请求出这条定直线的方程,如果不是,请说明理由
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com