
21.
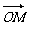
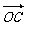 (本小题满分12分) 在平面直角坐标系中,O为坐标原点,已知两点M (1,-3)、N(5,1),若点C满足 =t +(1-t) (t∈R),点C的轨迹与抛物线:y2=4x交于A、B两点。
(本小题满分12分) 在平面直角坐标系中,O为坐标原点,已知两点M (1,-3)、N(5,1),若点C满足 =t +(1-t) (t∈R),点C的轨迹与抛物线:y2=4x交于A、B两点。

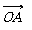 (1)求证: ⊥ ;
(1)求证: ⊥ ;
(2)在x轴上是否存在一点P (m,0),使得过点P任作抛物线的一条弦,并以该弦为直径的圆都过原点.若存在,请求出 m的值及圆心的轨迹方程;若不存在,请说明理由.
20.(本小题满分12分) 已知函数f(x)=x4-4x3+ax2-1在区间[0,1]上单调递增,在区间[1,2]上单调递减.
(1)求实数a的值;
(2)设g(x)=bx2-1,若关于x的方程f(x)=g(x)的解集恰有3个元素,求实数b的取值范围.
19.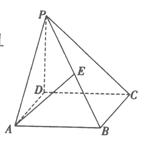 (本小题满分12分) 如图,在四棱维P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点.
(本小题满分12分) 如图,在四棱维P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点.
(1)求异面直线PD与AE所成角的大小;
(2)在平面PAD内求一点F,使得EF⊥平面PBC;
(3)在(2)的条件下,求二面角F-PC-E的大小.
18.(本小题12分)经统计,某大型商场一个结算窗口每天排队结算的人数及相应的概率如下:
|
排队人数 |
0-5 |
6-10 |
11-15 |
16-20 |
21-25 |
25人以上 |
|
概 率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
(1)每天不超过20人排队结算的概率是多少?
(2)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,请问该商场是否需要增加结算窗口?
17.(本小题满分12分) 在△ABC中,角A、B、C的对边分别为a、b、c, .
.
(1)求角C的大小;
(2)求△ABC的面积.
16.对于任意x∈R,若关于x的不等式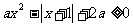 恒成立,则实数a的取值范围是______________.
恒成立,则实数a的取值范围是______________.
15.编辑一个运算程序:2*2006=1,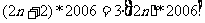 ,则2008*2006的输出结果为_____________.
,则2008*2006的输出结果为_____________.
|
|
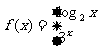 ,则
,则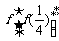 的值为_____________.
的值为_____________.14.已知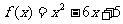 且,x,y满足
且,x,y满足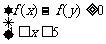 ,则
,则 的最大值__________.
的最大值__________.
12.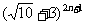 (n∈N*)的整数部分和小数部分分别为In和Fn,则Fn (Fn +In)的值为
(n∈N*)的整数部分和小数部分分别为In和Fn,则Fn (Fn +In)的值为
A.1 B.2 C.4 D.与n有关的数
11.使f(x)=sin(2x+y)+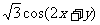 为奇函数,且在
为奇函数,且在 上是减函数的y的一个值是
上是减函数的y的一个值是
A.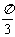 B.
B.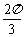 C.
C. D.
D.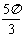
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com