
3. 下列符号中,既能表示氢元素,又能表示氢原子的是( )
A. 2H B. 2H+ C. 2H2 D. H
2. 下列物质中,属于纯净物的是( )
A. 澄清石灰水 B. 硫酸锌
C. 新鲜的空气 D. 钢
1. 下列变化中,属于化学变化的是( )
A. 白磷自燃 B. 汽油挥发
C. 水遇强冷变成冰 D. 分离液态空气制氧气
3.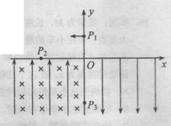 如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向。在x轴上方空间的第一、第二象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xy平面(纸面)向里的匀强磁场,在第四象限,存在沿y轴负方向、场强大小与第三象限电场场强相等的匀强电场。一质量为m、电荷量为q的带电质点,从y轴上y = h处的P1点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x = – 2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动。之后经过y轴上y = – 2h处的P3点进入第四象限。已知重力加速度为g。求:
如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向。在x轴上方空间的第一、第二象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xy平面(纸面)向里的匀强磁场,在第四象限,存在沿y轴负方向、场强大小与第三象限电场场强相等的匀强电场。一质量为m、电荷量为q的带电质点,从y轴上y = h处的P1点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x = – 2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动。之后经过y轴上y = – 2h处的P3点进入第四象限。已知重力加速度为g。求:
(1)粒子到达P2点时速度的大小和方向;
(2)第三象限空间中电场强度和磁感应强度的大小;
(3)带电质点在第四象限空间运动过程中最小速度的大小和方向。
4如图所示,PR是一块长为L=4 m的绝缘平板固定在水平地面上,整个空间有一个平行于PR的匀强电场E,在板的右半部分有一个垂直于纸面向外的匀强磁场B,一个质量为m=0.1 kg,带电量为q=0.5 C的物体,从板的P端由静止开始在电场力和摩擦力的作用下向右做匀加速运动,进入磁场后恰能做匀速运动。当物体碰到板R端的挡板后被弹回,若在碰撞瞬间撤去电场,物体返回时在磁场中仍做匀速运动,离开磁场后做匀减速运动停在C点,PC=L/4,物体与平板间的动摩擦因数为μ=0.4,取g=10m/s2 ,求:
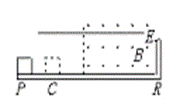 (1)判断物体带电性质,正电荷还是负电荷?
(1)判断物体带电性质,正电荷还是负电荷?
(2)物体与挡板碰撞前后的速度v1和v2
(3)磁感应强度B的大小
 (4)电场强度E的大小和方向
(4)电场强度E的大小和方向
5如图(甲)所示,两水平放置的平行金属板C、D相距很近,上面分别开有小孔 O和O',水平放置的平行金属导轨P、Q与金属板C、D接触良好,且导轨垂直放在磁感强度为B1=10T的匀强磁场中,导轨间距L=0.50m,金属棒AB紧贴着导轨沿平行导轨方向在磁场中做往复运动,其速度图象如图(乙),若规定向右运动速度方向为正方向.从t=0时刻开始,由C板小孔O处连续不断地以垂直于C板方向飘入质量为m=3.2×10 -21kg、电量q=1.6×10 -19C的带正电的粒子(设飘入速度很小,可视为零).在D板外侧有以MN为边界的匀强磁场B2=10T,MN与D相距d=10cm,B1和B2方向如图所示(粒子重力及其相互作用不计),求
(1)0到4.Os内哪些时刻从O处飘入的粒子能穿过电场并飞出磁场边界MN?
(2)粒子从边界MN射出来的位置之间最大的距离为多少?
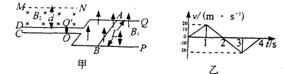
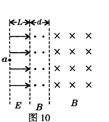 6如图所示,空间分布着有理想边界的匀强电场和匀强磁场,左侧匀强电场的场强大小为E、方向水平向右,其宽度为L;中间区域匀强磁场的磁感应强度大小为B、方向垂直纸面向外;右侧匀强磁场的磁感应强度大小也为B、方向垂直纸面向里。一个带正电的粒子(质量m,电量q,不计重力)从电场左边缘a点由静止开始运动,穿过中间磁场区域进入右侧磁场区域后,又回到了a点,然后重复上述运动过程。(图中虚线为电场与磁场、相反方向磁场间的分界面,并不表示有什么障碍物)。
6如图所示,空间分布着有理想边界的匀强电场和匀强磁场,左侧匀强电场的场强大小为E、方向水平向右,其宽度为L;中间区域匀强磁场的磁感应强度大小为B、方向垂直纸面向外;右侧匀强磁场的磁感应强度大小也为B、方向垂直纸面向里。一个带正电的粒子(质量m,电量q,不计重力)从电场左边缘a点由静止开始运动,穿过中间磁场区域进入右侧磁场区域后,又回到了a点,然后重复上述运动过程。(图中虚线为电场与磁场、相反方向磁场间的分界面,并不表示有什么障碍物)。
(1)中间磁场区域的宽度d为多大;
(2)带电粒子在两个磁场区域中的运动时间之比;
(3)带电粒子从a点开始运动到第一次回到a点时所用的时间t.
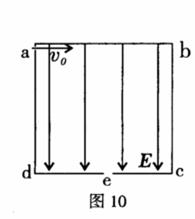
7如图所示,abcd是一个正方形的盒子,
在cd边的中点有一小孔e,盒子中存在着沿ad方向
的匀强电场,场强大小为E。一粒子源不断地从a处
的小孔沿ab方向向盒内发射相同的带电粒子,粒子
的初速度为v0,经电场作用后恰好从e处的小孔射出。
现撤去电场,在盒子中加一方向垂直于纸面的匀强磁
场,磁感应强度大小为B(图中未画出),粒子仍恰
好从e孔射出。(带电粒子的重力和粒子之间的相互作用力均可忽略)
(1)所加磁场的方向如何?
(2)电场强度E与磁感应强度B的比值为多大?
8如图所示,水平轨道与直径为d=0.8m的半圆轨道相接,半圆轨道的两端点A、B连线是一条竖直线,整个装置处于方向水平向右,大小为103V/m的匀强电场中,一小球质量m=0.5kg,带有q=5×10-3C电量的正电荷,在电场力作用下由静止开始运动,不计一切摩擦,g=10m/s2,
(1)若它运动的起点离A为L,它恰能到达轨道最高点B,求小球在B点的速度和L的值.
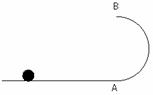 (2)若它运动起点离A为L=2.6m,且它运动到B点时电场消失,它继续运动直到落地,求落地点与起点的距离.
(2)若它运动起点离A为L=2.6m,且它运动到B点时电场消失,它继续运动直到落地,求落地点与起点的距离.
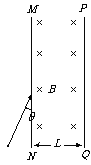 9如图所示,在真空区域内,有宽度为L的匀强磁场,磁感应强度为B,磁场方向垂直纸面向里,MN、PQ是磁场的边界。质量为m,带电量为-q的粒子,先后两次沿着与MN夹角为θ(0<θ<90º)的方向垂直磁感线射入匀强磁场B中,第一次,粒子是经电压U1加速后射入磁场,粒子刚好没能从PQ边界射出磁场。第二次粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场。不计重力的影响,粒子加速前速度认为是零,求:
9如图所示,在真空区域内,有宽度为L的匀强磁场,磁感应强度为B,磁场方向垂直纸面向里,MN、PQ是磁场的边界。质量为m,带电量为-q的粒子,先后两次沿着与MN夹角为θ(0<θ<90º)的方向垂直磁感线射入匀强磁场B中,第一次,粒子是经电压U1加速后射入磁场,粒子刚好没能从PQ边界射出磁场。第二次粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场。不计重力的影响,粒子加速前速度认为是零,求:
(1)为使粒子经电压U2加速射入磁场后沿直线运动,直至射出PQ边界,可在磁场区域加一匀强电场,求该电场的场强大小和方向。
(2)加速电压 的值。
的值。
10空间存在着以x=0平面为分界面的两个匀强磁场,左右两边磁场的磁感应强度分别为B1和B2,且B1:B2=4:3,方向如图所示。现在原点O处一静止的中性原子,突然分裂成两个带电粒子a和b,已知a带正电荷,分裂时初速度方向为沿x轴正方向,若a粒子在第四次经过y轴时,恰好与b粒子第一次相遇。求:
(1)a粒子在磁场B1中作圆周运动的半径与b粒子在磁场B2中圆周运动的半径之比。
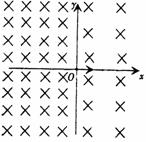 (2)a粒子和b粒子的质量之比。
(2)a粒子和b粒子的质量之比。
11如图1所示,真空中相距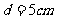 的两块平行金属板A、B与电源连接(图中未画出),其中B板接地(电势为零),A板电势变化的规律如图2所示
的两块平行金属板A、B与电源连接(图中未画出),其中B板接地(电势为零),A板电势变化的规律如图2所示
将一个质量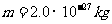 ,电量
,电量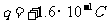 的带电粒子从紧临B板处释放,不计重力。求
的带电粒子从紧临B板处释放,不计重力。求
(1)在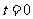 时刻释放该带电粒子,释放瞬间粒子加速度的大小;
时刻释放该带电粒子,释放瞬间粒子加速度的大小;
(2)若A板电势变化周期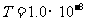 s,在
s,在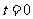 时将带电粒子从紧临B板处无初速释放,粒子到达A板时动量的大小;
时将带电粒子从紧临B板处无初速释放,粒子到达A板时动量的大小;
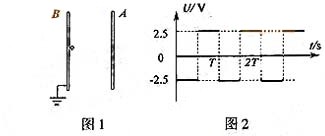 (3)A板电势变化频率多大时,在
(3)A板电势变化频率多大时,在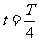 到
到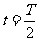 时间内从紧临B板处无初速释放该带电粒子,粒子不能到达A板。
时间内从紧临B板处无初速释放该带电粒子,粒子不能到达A板。
12如图所示,在足够大的空间范围内,同时存在着竖直向上的匀强电场和垂直纸面向里的水平匀强磁场,磁感应强度B=1.57T。小球1带正电,其电量与质量之比q1/m1=4C/kg,所受重力与电场力的大小相等;小球2不带电,静止放置于固定的水平悬空支架上。小球1向右以υ0=23.59m/s的水平速度与小球2正碰,碰后经过0.75s再次相碰。设碰撞前后两小球带电情况不发生改变,且始终保持在同一竖直平面内。(取g=10m/s2)
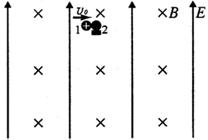 问:(1)电场强度E的大小是多少?
问:(1)电场强度E的大小是多少?
(2)两小球的质量之比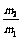 是多少?
是多少?
13在图示区域中,χ轴上方有一匀强磁场,磁感应强度的方向垂直纸面向里,大小为
B,今有一质子以速度v0由Y轴上的A点沿Y轴正方向射人磁场,质子在磁场中运动一段
时间以后从C点进入χ轴下方的匀强电场区域中,在C点速度方向与χ轴正方向夹角为
450,该匀强电场的强度大小为E,方向与Y轴夹角为450且斜向左上方,已知质子的质量为
m,电量为q,不计质子的重力,(磁场区域和电场区域足够大)求:
(1)C点的坐标。
(2)质子从A点出发到第三次穿越χ轴时的运动时间。
(3)质子第四次穿越χ轴时速度的大小及速度方向与电场E方向的夹角。(角度用反三角
函数表示)
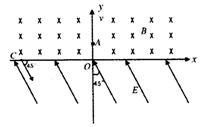
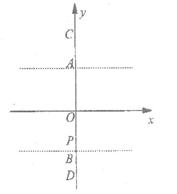 14图中y轴AB两点的纵坐标分别为d和-d。在0《y《d的区域中,存在沿y轴向上的非均匀电场,场强E的大小与y成正比,即E=ky;在y》d的区域中,存在沿y轴向上的匀强电场,电场强度F=kd(k属未知量)。X轴下方空间各点电场分布与x轴上方空间中的分布对称,只是场强的方向都沿y轴向下。现有一带电量为q质量为m的微粒甲正好在O、B两点之问作简谐运动。某时刻将一带电蕾为2q、质量为m的微粒乙从y轴上的c点处由静止释放,乙运动到0点和甲相碰并结为一体(忽略两微粒之间的库仑力)。在以后的运动中,它们所能达到的最高点和最低点分别为A点和D点,且经过P点时速度达到最大值(重力加速度为g)。
14图中y轴AB两点的纵坐标分别为d和-d。在0《y《d的区域中,存在沿y轴向上的非均匀电场,场强E的大小与y成正比,即E=ky;在y》d的区域中,存在沿y轴向上的匀强电场,电场强度F=kd(k属未知量)。X轴下方空间各点电场分布与x轴上方空间中的分布对称,只是场强的方向都沿y轴向下。现有一带电量为q质量为m的微粒甲正好在O、B两点之问作简谐运动。某时刻将一带电蕾为2q、质量为m的微粒乙从y轴上的c点处由静止释放,乙运动到0点和甲相碰并结为一体(忽略两微粒之间的库仑力)。在以后的运动中,它们所能达到的最高点和最低点分别为A点和D点,且经过P点时速度达到最大值(重力加速度为g)。
(1)求匀强电场E;
(2)求出AB间的电势差UAB及OB间的电势差UOB;
(3)分别求出P、C、D三点到0点的距离。
15如图所示,在绝缘水平面上,相距为L的A、B两点处分别固定着两个带电量相等的正电荷,a、b是AB连线上的两点,其中Aa=Bb=L/4,O为AB连线的中点,一质量为m带电量为+q的小滑块(可以看作质点)以初动能E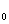 从a点出发,沿直线AB向b点运动,其中小滑块第一次经过O点时的动能为初动能的n倍(n>l),到达b点时动能恰好为零,小滑块最终停在O点,求:
从a点出发,沿直线AB向b点运动,其中小滑块第一次经过O点时的动能为初动能的n倍(n>l),到达b点时动能恰好为零,小滑块最终停在O点,求:
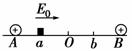 (1)小滑块与水平面间的动摩擦因数。
(1)小滑块与水平面间的动摩擦因数。
(2)O、b两点间的电势差U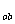 。
。
(3)小滑块运动的总路程。
2.(16分)如图甲所示,两个几何形状完全相同的平行板电容器PQ和MN,水平置于水平方向的匀强磁场中(磁场区域足够大),两电容器极板的左端和右端分别在同一竖直线上,已知P、Q之间和M、N之间的距离都是d,极板本身的厚度不计,板间电压都是U,两电容器的极板长相等。今有一电子从极板PQ中轴线左边缘的O点,以速度v0沿其中轴线进入电容器,并做匀速直线运动,此后经过磁场偏转又沿水平方向进入到电容器MN之间,且沿MN的中轴线做匀速直线运动,再经过磁场偏转又通过O点沿水平方向进入电容器PQ之间,如此循环往复。已知电子质量为m,电荷量为e。不计电容之外的电场对电子运动的影响。
(1)试分析极板P、Q、M、N各带什么电荷?
(2)求Q板和M板间的距离x ;
(3)若只保留电容器右侧区域的磁场,如图乙所示。电子仍从PQ极板中轴线左边缘的O点,以速度v0沿原方向进入电容器,已知电容器极板长均为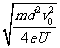 。则电子进入电容器MN时距MN中心线的距离?要让电子通过电容器MN后又能回到O点,还需在电容器左侧区域加一个怎样的匀强磁场?
。则电子进入电容器MN时距MN中心线的距离?要让电子通过电容器MN后又能回到O点,还需在电容器左侧区域加一个怎样的匀强磁场?
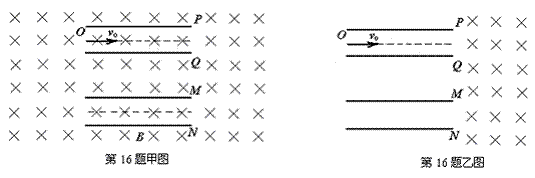
1.如图,在xOy平面内,MN和x轴之间有平行于y轴的匀强电场和垂直于xOy平面的匀强磁场,y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电荷量为e).如果电场和磁场同时存在,电子将做匀速直线运动.如果撤去电场,只保留磁场,电子将从x轴上距坐标原点3L的C点离开磁场.不计重力的影响,求:
(1)磁感应强度B和电场强度E的大小和方向;
(2)如果撤去磁场,只保留电场,电子将从D点(图中未标出)离开电场,求D点的坐标;
(3)电子通过D点时的动能.

14.解:物块与钢板碰撞时的速度
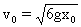 ①
①
设v1表示质量为m的物块与钢板碰撞后一起开始向下运动的速度,因碰撞时间极短,动量守恒,
mv0=2mv1 ②
刚碰完时弹簧的弹性势能为EP.当它们一起回到O点时,弹簧无形变,弹性势能为零,根据题给条件,这时物块与钢板的速度为零,由机械能守恒,
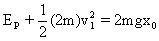 ③
③
设v2表示质量为2m的物块与钢板碰撞后开始一起向下运动的速度,则有
2mv0=3mv2 ④
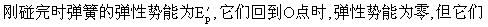
仍继续向上运动,设此时速度为v,则有
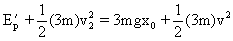 ⑤
⑤
在以上两种情况中,弹簧的初始压缩量都是x0,故有
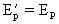 ⑥
⑥
当质量为2m的物块与钢板一起回到O点时,弹簧的弹力为零,物块与钢板只受到重力作用,加速度为g.一过O点,钢板受到弹簧向下的拉力作用,加速度大于g.由于物块与钢板不粘连,物块不可能受到钢板的拉力,其加速度仍为g.故在O点物块与钢板分离,分离后, 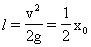 ⑦
⑦
12.解:(1)设A滑到a处的速度为v0= ①
f=uN,N=mg,f=ma,
a=ug ②
滑到板上离a点的最大距离为v02=2ugs0,
s0=2gh0/2ug=h0/u ③
A在板上不翻转应满足条件:摩擦力矩小于正压力力矩,即M摩擦≤M压力
umgR≤mg(L-s0) ④
h0≤u(L-Ur)=0.2(1-0.2)=0.16 m ⑤
(2)当h=0.45m,vA= = =3m/s
vA=vB=3m/s ⑥
设B在平板上运动直到平板翻转的时刻为t,取Δt=0.2s
sA=vA(t+Δt)-ug(t+Δt)2/2 ⑦’
sB=vBt-ugt2/2 ⑦
两物体在平板上恰好保持平板不翻转的条件是
2umgR=mg(L-sA)+mg(L-sB) ⑧
由⑦+⑦’式等于⑧式,得t=0.2s
13解.设质点P的质量为m,电量大小为q,根据题意,当A、B间的电压为U0时,有
qU0/d=mg,
当两板间的电压为2U0时,P的加速度向上,其大小为a,则
(q2U0/d)-mg=ma,
解得a=g.
当两板间的电压为零时,P自由下落,加速度为g,方向向下.
在t=0时,两板间的电压为2U0,P自A、B间的中点向上做初速度为零的匀加速运动,加速度为g.设经过时间τ1,P的速度变为v1,此时使电压变为零,让P在重力作用下做匀减速运动,再经过时间τ1′,P正好到达A板且速度为零,故有
v1=gτ1,0=v1-gτ1′,
(1/2)d=(1/2)gτ12+v1τ1′-(1/2)gτ1′2,
由以上各式,得
τ1=τ1′,τ1=(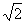 /2)
/2)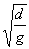 ,
因为t1=τ1,得t1=(
,
因为t1=τ1,得t1=(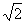 /2)
/2)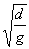 .
在重力作用下,P由A板处向下做匀加速运动,经过时间τ2,速度变为v2,方向向下,这时加上电压使P做匀减速运动,经过时间τ2′,P到达B板且速度为零,故有
v2=gτ2,0=v2-gτ2′,
d=(1/2)gτ22+v2τ2′-(1/2)gτ2′2,
由以上各式,得τ2=τ2′,τ2=
.
在重力作用下,P由A板处向下做匀加速运动,经过时间τ2,速度变为v2,方向向下,这时加上电压使P做匀减速运动,经过时间τ2′,P到达B板且速度为零,故有
v2=gτ2,0=v2-gτ2′,
d=(1/2)gτ22+v2τ2′-(1/2)gτ2′2,
由以上各式,得τ2=τ2′,τ2=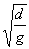 ,
因为t2=t1+τ1′+τ2,
得t2=(
,
因为t2=t1+τ1′+τ2,
得t2=(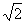 +1)
+1)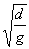 .
在电场力与重力的合力作用下,P由B板处向上做匀加速运动,经过时间τ3,速度变为v3,此时使电压变为零,让P在重力作用下做匀减速运动.经过时间τ3′,P正好到达A板且速度为零,故有
v3=gτ3,0=v3-gτ3′,
d=(1/2)gτ32+v3τ3′-(1/2)gτ3′2
由上得τ3=τ3′,τ3=
.
在电场力与重力的合力作用下,P由B板处向上做匀加速运动,经过时间τ3,速度变为v3,此时使电压变为零,让P在重力作用下做匀减速运动.经过时间τ3′,P正好到达A板且速度为零,故有
v3=gτ3,0=v3-gτ3′,
d=(1/2)gτ32+v3τ3′-(1/2)gτ3′2
由上得τ3=τ3′,τ3=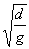 ,
因为t3=t2+τ2′+τ3,
得t3=(
,
因为t3=t2+τ2′+τ3,
得t3=(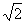 +3)
+3)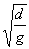 .
根据上面分析,因重力作用,P由A板向下做匀加速运动,经过时间τ2,再加上电压,经过时间τ2′,P到达B且速度为零,因为t4=t3+τ3′+τ2,
得t4=(
.
根据上面分析,因重力作用,P由A板向下做匀加速运动,经过时间τ2,再加上电压,经过时间τ2′,P到达B且速度为零,因为t4=t3+τ3′+τ2,
得t4=(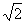 +5)
+5)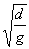 .
同样分析可得
tn=(
.
同样分析可得
tn=(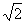 +2n-3)
+2n-3)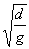 .(n≥2)
.(n≥2)
10、解.⑴当A球与弹簧接触以后,在弹力作用下减速运动,而B球在弹力作用下加速运动,弹簧势能增加,当A、B速度相同时,弹簧的势能最大。
设A、B的共同速度为v,弹簧的最大势能为E,则A、B系统动量守恒: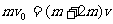 由机械能守恒:
由机械能守恒: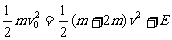 …②联立两式得:
…②联立两式得: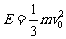 ……③
……③
⑵设B球与挡板碰撞前瞬间的速度为vB,此时A的速度为vA。系统动量守恒: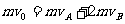 ………④
………④
B与挡板碰后,以vB向左运动,压缩弹簧,当A、B速度相同(设为v共)时,弹簧势能最大,为Em,则: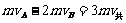 ……⑤
……⑤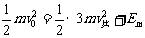 ……⑥由④⑤两式得:
……⑥由④⑤两式得: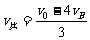 代入⑥式,化简得:
代入⑥式,化简得: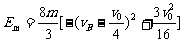 ⑦而当弹簧恢复原长时相碰,vB有最大值vBm,则: mv0=mvA′+2mvBm
mv02/2=mvA′2/2+2mvBm2/2 联立以上两式得:vBm=
⑦而当弹簧恢复原长时相碰,vB有最大值vBm,则: mv0=mvA′+2mvBm
mv02/2=mvA′2/2+2mvBm2/2 联立以上两式得:vBm=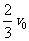 即vB的取值范围为:
即vB的取值范围为: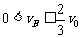 ⑧
⑧
结合⑦式可得:当vB=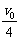 时,Em有最大值为:
时,Em有最大值为: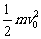 …⑨ 当vB=
…⑨ 当vB=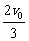 时,Em有最小值为:
时,Em有最小值为: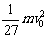 ⑩
⑩
11解:由牛顿第二定律在平衡位置可建立方程:
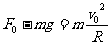 ①------(2分)在最大偏角处可建立方程:
①------(2分)在最大偏角处可建立方程: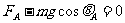 ②------(2分)
②------(2分)
其中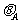 为最大偏角,FA为小滑块运动至最大偏角时所受支持力,由机械能守恒得:
为最大偏角,FA为小滑块运动至最大偏角时所受支持力,由机械能守恒得: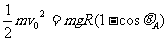 ③------(3分)
③------(3分)
由①②③式解得小滑块的质量和最大偏角分别为: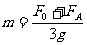 ④------(1分)
④------(1分)
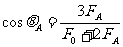 ⑤------(1分)由图线读得数可知,在t=0.1s时,小滑块第一次运动到平衡位置,对碗的压力F0=1.6N;在t=0.6s时,小滑块第一次运动到最大偏角位置,对碗的压力FA=0.1N;由④⑤式可得m=60g,cos
⑤------(1分)由图线读得数可知,在t=0.1s时,小滑块第一次运动到平衡位置,对碗的压力F0=1.6N;在t=0.6s时,小滑块第一次运动到最大偏角位置,对碗的压力FA=0.1N;由④⑤式可得m=60g,cos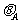 =1/6.
------(2分)
=1/6.
------(2分)
从以上分析可以得出以下判断:(1)小球的质量m=60g;(2)由于摆幅很大,故小球在碗中来回滑动虽近似周期运动,T=2.0s;但不是简谐运动。------(2分)
9、解:(1)子弹击中滑块A的过程中,子弹与滑块A组成的系统动量守恒
mC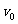 =(mC+mA)vA
=(mC+mA)vA 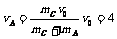
(2)对子弹滑块A、B和弹簧组成的系统,A、B速度相等时弹性势能最大。
根据动量守恒定律和功能关系可得:
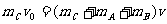
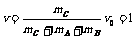
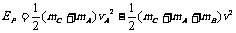 =6 J
=6 J
(3)设B动能最大时的速度为 vB′,A的速度为vA′,则
vB′,A的速度为vA′,则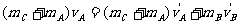
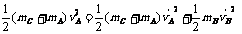
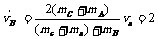 B获得的最大动能
B获得的最大动能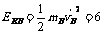
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com