
4.2010年上海世博会丹麦国家馆,有一尊“小美人鱼”铜像。(5分)
(1)“小美人鱼”故事出自哪位作家的哪篇作品?
(2)请以“小美人鱼”口吻,写一段不超过30个字的话,表达对上海世博会的祝愿或赞美
2.下列各句中,加点的成语使用恰当的一句是(3分)
A.司机张师傅冒着生命危险解救乘客的事迹,一经新闻媒体报道,就被传得满城风雨,感动了无数市民。
B.近年来,在种种灾害面前,各级政府防患未然,及时启动应急预案,力争把人民的生命财产损失降到最低限度。
C.这些“环保老人”利用晨练的机会,将游客丢弃在景点的垃圾信手拈来,集中带到山下,分类处理。
D.“生命的价值在于厚度而不在于长度,在于奉献而不在于获取……”院士的一番话入木三分,让我们深受教育。
1.下列加点的字,每对读音都不相同的一组是(3分)
A.弹劾/弹丸之地 哽咽/狼吞虎咽 责难/多难兴邦
B.鲜活/寡廉鲜耻 泊位/淡泊明志 叶韵/一叶知秋
C.大度/审时度势 长进/身无长物 解救/浑身解数
D.参差/扪参历井 披靡/风靡一时 畜牧/六畜兴旺
(11)命题“对任何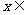 R,
R,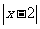 +
+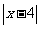 >3”的否定是 .
>3”的否定是 .
 (12)(
(12)(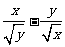 )
)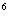 的展开式中,
的展开式中,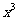 的系数等于 .
的系数等于 .
(13) 设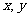 满足约束条件
满足约束条件 若目标函数
若目标函数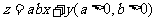 的最大值为8,则
的最大值为8,则 的最小值为 。
的最小值为 。
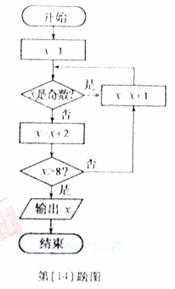
(14) 如图所示,程序框图(算法流程图)的输出值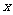 =
=
(15) 甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球。先从甲罐中随机取出一球放入乙罐,分别以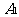 ,
,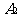 和
和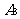 表示由甲罐取出的球是红球,白球和黑球的事件。再从乙罐中随机取出一球,以B表示由乙罐取出的球是红球的事件。则下列结论中正确的是 (写出所有正确结论的编号)
表示由甲罐取出的球是红球,白球和黑球的事件。再从乙罐中随机取出一球,以B表示由乙罐取出的球是红球的事件。则下列结论中正确的是 (写出所有正确结论的编号)
①P(B)=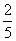 ;
;
②P(B|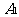 )=
)=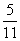 ;
;
③事件B与事件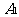 相互独立;
相互独立;
④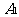 ,
,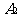 ,
,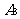 是两两互斥的事件;
是两两互斥的事件;
⑤P(B)的值不能确定,因为它与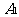 ,
,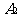 ,
,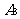 中究竟哪一个发生有关;
中究竟哪一个发生有关;
三:解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。解答时写在答题卡的指定区域内。
(16)(本小题满分12分)
设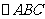 是锐角三角形,a、b、c分别是内角A、B、C所对边长,并且
是锐角三角形,a、b、c分别是内角A、B、C所对边长,并且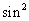 A=sin(
A=sin(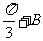 )sin(
)sin(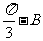 )+
)+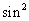 B。
B。
(Ⅰ)求角A的值;
(Ⅱ)若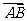 ·
·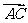 =12,a=2
=12,a=2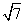 ,求b、c(其中b<c)。
,求b、c(其中b<c)。
(17)(本小题满分12分)
设a为实数,函数f(x)=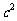 -2x+2a,x
-2x+2a,x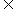 R.
R.
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)求证:当a>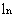 2-1且x>0时,
2-1且x>0时,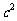 >
>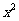 -2ax+1
-2ax+1
(18) (本小题满分13分)
如图,在多面体ABCDEF中,四边形ABCD是正方形,EF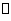 AB,EF
AB,EF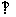 FB, AB=2EF,
FB, AB=2EF,
 BFC=90°,BF
BFC=90°,BF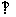 FC,H为BC的中点。
FC,H为BC的中点。
(Ⅰ)求证:FH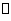 平面EDB;
平面EDB;
(Ⅱ)求证:AC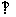 平面EDB;
平面EDB;
(Ⅲ)求二面角B-DE-C的大小
(19)(本小题满分13分)
已知椭圆E经过点A(2.,3),对称轴为坐标轴,焦点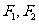 在x轴上,离心率c=
在x轴上,离心率c=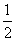
(Ⅰ)求椭圆E的方程;
(Ⅱ)求∠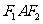 的角平分线所在直线l的方程
的角平分线所在直线l的方程
(Ⅲ)在椭圆E上是否存在关于直线l对称的相交两点?若存在,请找出,若不存在,说明理由。
(20)(本小题满分12分)
设数列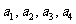 ……
……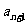 中每一项都不为0
中每一项都不为0
证明,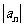 为等差数列的充分必要条件是:对任何
为等差数列的充分必要条件是:对任何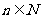 ,都有
,都有
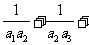 ……
……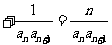
(21)(本小题满分13分)
品酒师需定期接受酒味鉴别功能测试,一般通常采用的测试方法如下:拿出n瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n瓶酒,并重新按品质优劣为它们排序,这成为一轮测试,根据一轮测试中的两次排序的偏离程度的高低为其评分.
现设n=4,分别以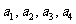 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
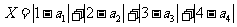
则X是对两次排序的偏离程度的一种描述。
(Ⅰ)写出X的可能值集合;
(Ⅱ)假设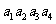 等可能地为1.2.3.4的各种排列,求X的分布列;
等可能地为1.2.3.4的各种排列,求X的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中都有X≤2,
(ⅰ)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ⅱ)你认为该品酒师的酒味鉴别功能如何?说明理由。
(1)
i 是虚数单位,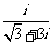 =
=
(A)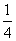 -
-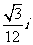 (B)
(B)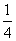 +
+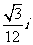 (C)
(C)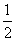 +
+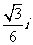 (D)
(D)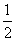 -
-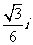
(2)若合计A={x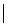
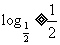 },则
},则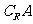 =
=
(A)(-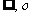 ]
]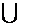 (
(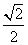 ,+
,+ ) (B)(
) (B)(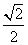 , +
, + )
)
(C)(-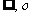 ]
]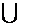 [
[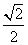 ,+
,+ )
(D)[
)
(D)[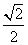 , +
, + )
)
(3)设向量a=(1,0),b=(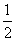 ,
,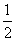 ),则下列结论中正确的是
),则下列结论中正确的是
(A)|a|=|b|
(B)a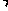 b =
b =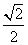
(C)a-b 与b垂直 (D)a//b
(4).若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)-f(4)=
(A)-1 (B) 1 (C) -2 (D) 2
(5).双曲线方程为x2 - 2y2=1,则它的右焦点坐标为
(A)(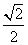 ,0) (B) (
,0) (B) (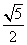 ,0) (C)
(
,0) (C)
(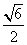 ,0) (D) (
,0) (D) (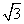 ,0)
,0)
(6).设abc>0,二次函数f(x)=ax2+bx+c的图象可能是
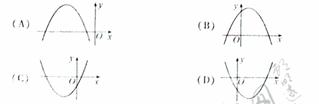
(7)设曲线C的参数方程为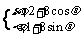 (
( 为参数),直线l的方程为
为参数),直线l的方程为 ,则曲
,则曲
线C到直线l距离为的点的个数为
(A)1 (B)2
 (C)3
(D)4
(C)3
(D)4
(8)一个几个何体的三视图如图,该几何体的表面积为
(A)280 (B)292
(C)360 (D)372
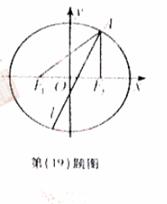
(9)动点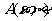 在圆
在圆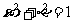 上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,
上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,
已知时间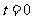 时,点
时,点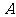 的坐标是
的坐标是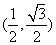 ,则当
,则当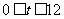 时,动点
时,动点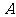 的纵坐标
的纵坐标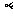 关于
关于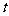 (单位:秒)的函数的单调递增区向是
(单位:秒)的函数的单调递增区向是
(A)[0,1] (B)[1,7]
(C)[7,12] (D)[0,1]和[7,12]
(10)设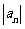 是任意等比数列,它的前
是任意等比数列,它的前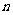 项和,前2
项和,前2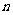 项和与前3
项和与前3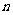 项和分别为
项和分别为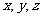 ,则下列等式中恒成立的是
,则下列等式中恒成立的是
(A)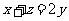 (B)
(B)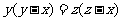
(C)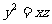 (D)
(D)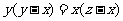
(在此卷上答题无效)
2010年普通高等学校招生全国统一考试(安徽卷)
数 学(理科)
第Ⅱ卷(非选择题 共100分)
请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效.
22.请依照下面的例句,从雨鞋、桌布、月亮、太阳这四个意象中任选两个,分别
写一句含有哲理情思的话语。(4分)
(例句)雨伞:你不能为别人挡风遮雨,谁会把你举在头顶上?
答:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com