
祝考試順利
第壹部分:選擇題(佔77分)
|
1 H 1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 He 4.0 |
|
3 Li 6.9 |
4 Be 9.0 |
|
|
|
|
|
|
|
|
|
|
5 B 10.8 |
6 C 12.0 |
7 N 14.0 |
8 O 16.0 |
9 F 19.0 |
10 Ne 20.2 |
|
11 Na 23.0 |
12 Mg 24.3 |
|
|
|
|
|
|
|
|
|
|
13 Al 27.0 |
14 Si 28.1 |
15 P 31.0 |
16 S 32.1 |
17 Cl 35.5 |
18 Ar 40.0 |
|
19 K 39.1 |
20 Ca 40.1 |
21 Sc 45.0 |
22 Ti 47.9 |
23 V 50.9 |
24 Cr 52.0 |
25 Mn 54.9 |
26 Fe 55.8 |
27 Co 58.9 |
28 Ni 58.7 |
29 Cu 63.5 |
30 Zn 65.4 |
31 Ga 69.7 |
32 Ge 72.6 |
33 As 74.9 |
34 Se 79.0 |
35 Br 79.9 |
36 Kr 83.8 |
7、已知数列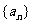 的前
的前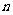 项和为
项和为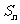 ,对一切正整数
,对一切正整数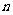 ,点
,点 都在函数
都在函数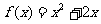 的图像上,且过点
的图像上,且过点 的切线的斜率为
的切线的斜率为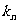 .
.
(1)求数列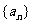 的通项公式
的通项公式
(2)若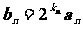 ,求数列
,求数列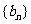 的前
的前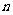 项和
项和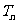 .
.
(3)设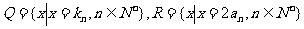 ,等差数列
,等差数列 的任一项
的任一项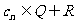 ,其中
,其中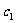 是
是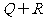 中的最小数,
中的最小数,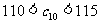 ,求
,求 的通项公式.
的通项公式.
6.数列 满足:
满足: ,则
,则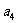 = ;若
= ;若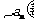 有一个形如
有一个形如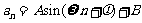 的通项公式,其中A, B,
的通项公式,其中A, B, 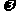 ,
,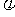 均为实数,且
均为实数,且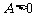 ,
, ,
,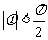 ,则此通项公式可以为
,则此通项公式可以为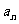 =
(写出一个即可).
=
(写出一个即可).
5.在数列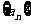 中,如果存在非零常数T,使得
中,如果存在非零常数T,使得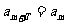 对任意正整数m均成立,那么就称
对任意正整数m均成立,那么就称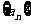 为周期数列,其中T叫做数列
为周期数列,其中T叫做数列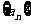 的周期。已知数列
的周期。已知数列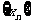 满足
满足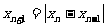
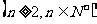 ,且
,且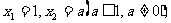 当数列
当数列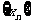 周期为3时,则该数列的前2007项的和为
.
周期为3时,则该数列的前2007项的和为
.
4.已知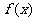 是定义在R上的不恒为零的函数,且对任意
是定义在R上的不恒为零的函数,且对任意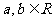 满足下列关系式:
满足下列关系式:
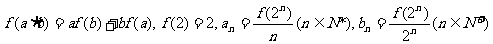 ,考察下列结论:①
,考察下列结论:①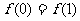 ②
②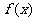 为偶函数③数列
为偶函数③数列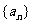 为等比数列④数列
为等比数列④数列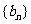 为等差数列,其中正确的结论是
为等差数列,其中正确的结论是
3.椭圆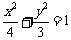 上有n不同的点
上有n不同的点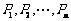 ,椭圆的右焦点为
,椭圆的右焦点为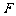 ,数列
,数列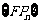 是公差大于
是公差大于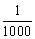 的等差数列,则n的最大值为 .
的等差数列,则n的最大值为 .
2.对正整数n,设曲线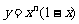 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为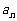 ,则数列
,则数列 的前n项和的公式是
.
的前n项和的公式是
.
1.已知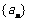 是递增数列,且对任意
是递增数列,且对任意 都有
都有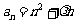 成立,实数
成立,实数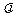 取值范围是
取值范围是
8. 
三 范例剖析
例1 已知定义域为R的二次函数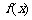 的最小值为0且有
的最小值为0且有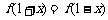 ,直线
,直线
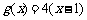 被
被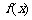 的图像截得的弦长为
的图像截得的弦长为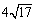 ,数列
,数列 满足
满足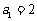 ,
,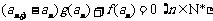 .
.
(1)函数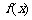 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)设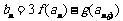 ,求数列
,求数列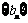 的最值及相应的n.
的最值及相应的n.
例2 设A(x1,y1),B(x2,y2)是函数f(x)=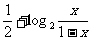 的图象上任意两点,且
的图象上任意两点,且
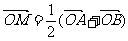 ,已知点M的横坐标为
,已知点M的横坐标为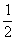 .
.
(1)求证:M点纵坐标为定值; 若Sn=f(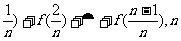 ∈N*,且n≥2,求Sn;
∈N*,且n≥2,求Sn;
(2)已知an=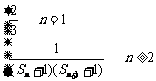 ,其中n∈N*.
,其中n∈N*.
Tn为数列{an}的前n项和,若Tn<λ(Sn+1+1)对一切n∈N*都成立,试求λ的取值范围.
例3 (08山东卷)将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:
a1
a2 a3
a4 a5 a6
a7 a8 a9 a10
……
记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1. Sn为数列{bn}的前n项和,且满足=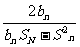 1=(n≥2).
1=(n≥2).
(Ⅰ)证明数列{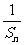 }成等差数列,并求数列{bn}的通项公式;
}成等差数列,并求数列{bn}的通项公式;
(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当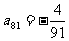 时,求上表中第k(k≥3)行所有项和的和.
时,求上表中第k(k≥3)行所有项和的和.
四 巩固训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com