19．(本小题满分14分)

　　 已知函数f (x) = ，x∈[1,+¥].

　 (I)当 a = 时，求函数 f (x) 的最小值；

　 (II)若对任意 x∈[1,+¥)，f (x) > 0 恒成立，试求实数 a 的取值范围.

18．(本小题满分14分)

　　 已知函数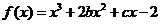的图象在与轴交点处的切线方程是.

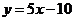　 (I)求函数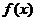的解析式；

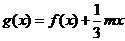　 (II)设函数，若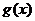的极值存在，求实数的取值范围以及函数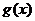取得极值时对应的自变量的值.

17．(本小题满分14分)

某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元．

　 (I)当一次订购量为多少个时，零件的实际出厂单价恰降为51元?

　 (II)设一次订购量为x个，零件的实际出厂单价为P元，求出函数 P = f (x) 的表达式.

16．(本小题满分12分)

　　 若存在过点(1, 0)的直线与曲线y=x³和y=ax²+ x－9都相切，求的值．

15．(本小题满分12分)

　已知在平面直角坐标系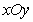中的一个椭圆，它的中心在原点，左焦点为,

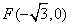右顶点为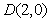,设点.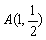

(1)求该椭圆的标准方程；

(2)若是椭圆上的动点，求线段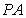中点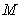的轨迹方程。

14．若函数 f (x) 在[0，1]上满足：对于任意的 s、t∈[0,+¥]，l >0, 都有 <f ( )，则称 f (x) 在[0，1]上为凸函数。

在三个函数 f₁(x) = x－1，f₂(x) = 2 ^x－1，f₃(x) = ln 　中，在[0，1]上是凸函数的

有 　　　(写出您认为正确的所有函数)。

13．已知函数 f (x)=2^x+x，g(x)=log₂x+x，h(x)=log₂x－2的零点依次为a, b, c，则a, b, c的大小关系是　　 。

12．函数 y = lg(x²+3kx+k²+5)的值域为R，则k的取值范围是 　　　。

11．若函数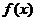是定义在(0，+)上的增函数，且对一切x>0,y>0满足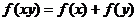，则不等式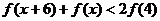的解集为__　　　　 .

10. P是双曲线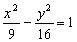的右支上一点，M、N分别是圆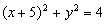和

圆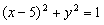的圆心，则|PM|+|PN|的最小值为　　

　 A. 8　　　 B.9　　　 C.10　　　 D.16