1. 下面是科学家探索基因的历程，

　　 ①1866年孟德尔的豌豆杂交实验：提出遗传因子(基因)

　　 ②1903年萨顿研究蝗虫的精子和卵细胞形成过程，提出假说：基因在染色体上

③1910年摩尔根进行果蝇杂交实验：找到基因在染色体上的实验证据

　 他们在研究的过程所使用的科学研究方法依次为　　　　　　　　　　　　　 　

　A．①假说一演绎法 ②假说一演绎　 　③类比推理

B．①假说一演绎法 ②类比推理　　 　③类比推理

　C．①假说一演绎法 ②类比推理 　　③假说一演绎法

D．①类比推理 　　②假说一演绎法 ③类比推理

　 2．对于下列式子，正确的说法有　　　　　　　　　

①表示DNA复制过程；　　 ②表示DNA转录过程；　 ③式中共有5种碱基；

④式中共有8种核苷酸　 　⑤式中共5种核苷酸　 　　⑥式中的A均代表同一种核苷酸

A．①②③　　　　 B．②⑤⑥　　　 C．②③④　　　　　 D．①③⑤

19、(本小题13分)已知, 其中向量，点 在的图像上, 且点为的图像与轴的交点.若数列为等差数列, 且公差为1, .

　 (1) 求数列, 的通项公式;

　 (2) 求的最小值;

　 (3) 记, 且，问是否存在，使得？若存在，求出的值；若不存在，说明理由.

解: (1) 由, , 得:

　 …………………… (1)

即　

为与轴的交点,　

　 则 　　

20、(本小题14分)已知函数.

(1)求函数的单调递增区间；

(2)数列满足：，且,记数列的前n项和为，且；试求：

①求数列的通项公式；并判断是否仍为数列中的项？若是，请证明；否则，说

明理由.

②记，求数列的前项和 .

当时，，

当时，，

所以.　　　　　　　 　　……………………………(8分)

又因为，

所以令，则

得到与矛盾，所以不在数列中. 　　………(10分)

的逆矩阵．

解： ，即 ，

所以　 得　　　　　 　　……………………(4分)

　　 即M= 　，由得 .

或 =1 , 　.　　　　 　　……………………(7分)

(2)(选修4－4：极坐标及参数方程)

已知曲线C的极坐标方程是，设直线l的参数方程是(t为

参数)．判断直线l和曲线C的位置关系．

16、(本小题13分)已知函数的图象在点B(1，)处的切线的斜率为－3.

(1)求、的值；

(2)若不等式对于恒成立，求的取值范围.

图像与函数相邻两交点间的距离为　

　即…………5分 …………7分

　 (2)由平移公式得

得平移后的解析式为…………9分

平移后的图像关于原点对称　　 …………11分

时，的最小值为…………13分。

∴⊥，而EF平面ACD₁，

∴EF∥平面ACD₁……………………………………………………(6分)

(2) ∵=(0,2，0)，cos<,>=

∴异面直线EF与AB所成角的余弦值为……………………(9分).

(3)设点P(2，2，t)(0<t≤2)，平面ACP的一个法向量为=(x，y，z)，

解法二：(1)同解法一知=(-1,2，-1) ，=(-2,0，2)，

= (-2,2，0)，∴-=，

∴、、共面.

又∵EF平面ACD₁，∴EF∥平面ACD₁. ……………………………(6分)

(2)、(3)同解法一．

解法三：(1)取AD₁的中点K，连结EK、KC，在△AA₁D₁

中，EK∥AA₁，且EK=AA₁，

　 ∵FC=CC₁，CC₁∥AA₁，∴FC　　 EK，

∴四边形EKCF为平行四边形，

∴EF∥CK．又∵CK平面ACD₁，

EF平面ACD₁，∴EF∥平面ACD₁. (4分)

二面角P-AC-B的大小为30°. ……………………………………(13分)

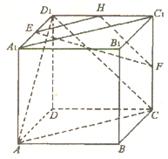解法四：(1)取D₁C₁的中点H，连结EH，FH，A₁C₁，

　　　　　 ∵E为A₁D₁的中点，∴EH∥A_lC_l，

　　　　　 而A₁C₁∥AC，∴EH∥AC，

　　　　　 又∵F为CC₁的中点，∴HF∥D₁C．

　　　　　 ∵EH与HF相交，D₁C与AC相交，

　　　　　 ∴平面EHF∥平面ACD₁，EF平面EHF，

　　　　　 ∴EF∥平面ACD₁．　 ………………(4分)

　　　　　 (2)、(3)同解法三．

成立，则实数t的取值范围是　 　　　　　　　　　.

9、设定义域为R的函数满足下列条件：① 对任意；② 对任意，则下列不等式不一定成立的是(　 C　 )

10、若一个数列的各项都是实数，且从第二项开始，每一项与它前一项的平方差是相同的常数，则称该数列为等方差数列，这个常数叫做这个数列的公方差.设数列是首项为2，公方差为2的等方差数列，若将这种顺序的排列作为某种密码，则这种密码的个数为(　 A　 )

A.　 512个　　　　　　　　 B. 513个　　　　　　 C.　 1024个　 　　　　 D. 1025个

第Ⅱ卷(非选择题 共100分)

4、一个空间几何体的三视图及部分数据如图所示，

则这个几何体的体积是　 _{(　 D　 )}

A．3　　 　　　 B．　 　　　　 C．2　　 　　　 D．_{[来源:Z§X§X§K]}

①函数在区间上是减函数；

②直线是函数图象的一条对称轴；

③函数 的图象可由函数的图象向左平移而得到；

④若 　，则 的值域是.　

其中正确命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　 ( B　　 )

A．1　　　　　　　 B．2　 　　　　　　C．3 　　　　　　　　D．4

3、对于两条直线a,b和平面的　　　　　　　　　　　　 (　 D　 )

　　 A．充分但不必要条件　　　　　　　 B．必要但不充分条件

C．充要条件　　 　　　　　　　　 D．既不充分也不必要条件

2、正项等比数列中，若，则等于　　　　　　　　　　 　( C　　 )

　　 A. -16　 　　　　　　 B. 10　　　　　　　 C. 16　　　　　　　 D. 256

1、积分的值是　　　　　　　　　　　　　　　　　　　　　　　　　 (　 D　 )

A. 1　　　　　　　 B. e　　　　　　　　 C. e+1　　　　　　　 D. e²

21、本题有(1)、(2)、(3)三个小题，每题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分。

(1)(选修4－2：矩阵与变换)

若点在矩阵　　 　对应变换的作用下得到的点为，求矩阵的逆矩阵．

(2)(选修4－4：极坐标及参数方程)

已知曲线C的极坐标方程是，设直线l的参数方程是(t为参数)．判断直线l和曲线C的位置关系．

(3)(选修4－5：不等式选讲)

已知≤1的解集为，若关于x的不等式恒成立，求实数a的取值范围.

漳州三中2010届高三年第四次月考理科数学试卷

第Ⅰ卷(选择题 共50分)答案