21．(本小题满分14分)

对于函数，若存在R，使成立，则称为的不动点.如果函数N^*有且仅有两个不动点0和2，且

　 (1)求实数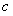，的值；

　 (2)已知各项不为零的数列，并且，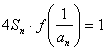

求数列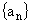的通项公式；；

　 (3)求证：.

2009年秋季湖北省部分重点中学期中联考

20．(本小题满分13分)

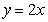　 已知二次函数的图象与轴相切于点，其导函数与直线平行.

　 (1)求的解析式；

　 (2)已知，试讨论方程在区间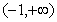

　　　　 上解得个数。

19．(本小题满分12分)

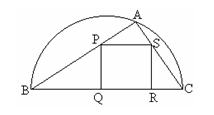如图，某园林单位准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余的地方种花.若BC＝a，∠ABC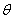＝，设△ABC的面积为S₁，正方形的面积为S₂．

(1)用a、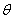表示S₁和S₂；

(2)当a固定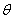，变化时，求取最小值时的角.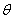

18．(本小题满分12分)

　　 已知函数其中.

(Ⅰ)若函数没有零点，求实数的取值范围；

(Ⅱ)求函数的单调区间与极值

17．(本小题满分12分)

已知等比数列中，，公比，又分别是某等差数列的第7项，第3项，第1项.

　 (1)求的通项公式；

　 (2)设，求数列的前项和

16．(本小题满分12分)

若函数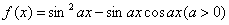的图象与直线相切，并且切点的横坐标依次成公差为的等差数列.

　 (1)求的值；

(2)若点是图象的对称中心，且，求点的坐标.

15．如果数列，就称数列为和比数列，下列四个说法中：

　　 ①若是等比数列，则是和比数列；

②设，若是和比数列，则也是和比数列；

③存在等差数列，它也是和比数列；

④设，若是和比数列，则也是和比数列.

其中正确的说法是__________.

14．已知且在区间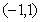内是单调函数，则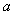的取值范围是__________.

13．为锐角三角形，若角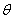终边上一点P的坐标为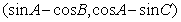，则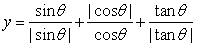的值为___________.

12．二次函数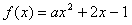的值域是，那么函数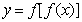的值域是________.