
21.已知二次函数 ,当
,当 上有最小值
上有最小值 ,试求
,试求 的解析式及函数
的解析式及函数 的值域。
的值域。
20.已知函数 ,且
,且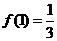 ,
,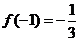 。
。
(1)求函数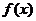 的解析式
的解析式
(2)判断函数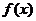 在定义域上的单调性,并证明。
在定义域上的单调性,并证明。
19.已知函数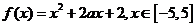
(1)当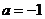 时,求函数的最大值和最小值;
时,求函数的最大值和最小值;
(2)求实数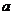 的取值范围,使
的取值范围,使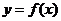 在区间
在区间 上是单调函数
上是单调函数
18.(1)设 ,
,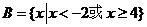 .求
.求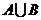 、
、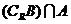 。
。
(2)设集合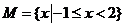 ,
,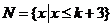 ,若
,若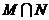
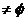 ;请用集合形式表示
;请用集合形式表示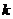
的取值范围。
17.已知全集 ,
,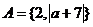 ,
,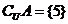 ,求
,求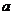 的值。
的值。
16、函数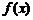 定义域为D,
若存在
定义域为D,
若存在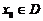 使
使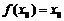 , 则称
, 则称 为函数
为函数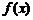 图象上的不动点;则求函数
图象上的不动点;则求函数 的图象上不动点的坐标为
.
的图象上不动点的坐标为
.
15、已知集合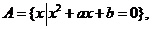
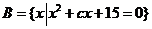 ,且
,且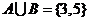 ,
, ,则实数
,则实数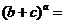
14、已知函数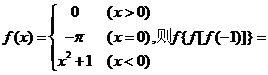
13、设集合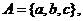 集合
集合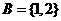 ,则从
,则从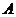 到
到 的映射有 个。(用数字作答)
的映射有 个。(用数字作答)
12、 如图所示的是某池塘中的浮萍蔓延的面积(
如图所示的是某池塘中的浮萍蔓延的面积( )与时间
)与时间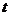 (月)
(月)
的关系: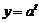 ,有以下叙述:
,有以下叙述:
① 这个指数函数的底数是2;
② 第5个月时,浮萍的面积就会超过 ;
;
③ 浮萍从 蔓延到
蔓延到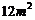 仅需要经过1.5个月;
仅需要经过1.5个月;
④ 浮萍每个月增加的面积都相等
其中正确的是( )。
A.①②③ B.①②③④ C.②③④ D.①②
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com