
 1.
研究物理问题时,常常需要忽略某些次要因素,建立理想化的物理模型。例如“质点”模型忽略了物体的体积、形状,只计算质量。请再写出两个你所学过的物理模型的名称:(1)
。(2)
1.
研究物理问题时,常常需要忽略某些次要因素,建立理想化的物理模型。例如“质点”模型忽略了物体的体积、形状,只计算质量。请再写出两个你所学过的物理模型的名称:(1)
。(2)
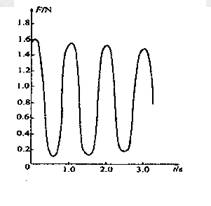
2. 将一个力传感器连接到计算机上,我们
就可以测量快速变化的力。幽中所示就
是用这种方法测得的小滑块在半球形碗
内在竖直平面内来回滑动时,对碗的压
力大小随时间变化的曲线。从这条曲线
提供的信息,可以判断滑块大约每隔
s经过碗底一次;滑块滑
动过程中机械能
(填“守恒”或“不守恒”)
23.(本题满分18分)第(1)题4分,第(2)题5分,第(3)题9分。
对于定义域为D的函数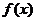 同时满足条件:(1)常数a,b满足
同时满足条件:(1)常数a,b满足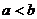 ,区间[a,b]
,区间[a,b]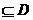 ,(2)使
,(2)使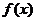 在[a,b]上的值域为
在[a,b]上的值域为 ,那么我们把
,那么我们把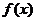 叫做[a,b]上的“k级矩形”函数。
叫做[a,b]上的“k级矩形”函数。
(1)设函数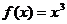 是[a,b]上的“1级矩形”函数,求常数a,b的值;
是[a,b]上的“1级矩形”函数,求常数a,b的值;
(2)是否存在常数a,b与正数k,使函数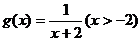 在区间[a,b]上的是“k级矩形”函数?若存在,求出a,b及k的值,若不存,说明理由。
在区间[a,b]上的是“k级矩形”函数?若存在,求出a,b及k的值,若不存,说明理由。
(3)设 是[a,b]上“3级矩形”函数,求出常数a,b的值。
是[a,b]上“3级矩形”函数,求出常数a,b的值。
22.(本题满分18分)第(1)题4分,第(2)题6分,第(3)题8分。
设函数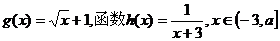 ,其中a为常数且
,其中a为常数且 ,令函数
,令函数 的积函数。
的积函数。
(1)求函数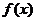 的表达式,并求其定义域。
的表达式,并求其定义域。
(2)当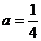 时,求函数
时,求函数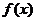 的值域。
的值域。
(3)是否存在自然数a,使得函数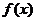 的值域恰为
的值域恰为 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由。
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由。
21.(本小题满分16分)第(1)题8分,第(2)题8分。
已知函数
(1)求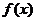 的最大值和最小值;
的最大值和最小值;
(2)若不等式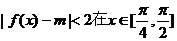 上恒成立,求实数m的取值范围。
上恒成立,求实数m的取值范围。
20.(本小题满分14分)第(1)小题8分,第(2)小题6分。
为了保护一种珍贵文物,博物馆需要在一种无色玻璃的密封保护罩内充入保护气体。假设博物馆需要支付的总费用由两部分组成:①罩内该种气体的体积比保护罩的容积少0.5立方米,且每立方米气体费用为1千元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为8千元。
(1)求博物馆支付总费用y与保护罩容积V之间的函数关系式;
(2)求博物馆支付总费用的最小值。
19.(本小题满分12分)
解不等式: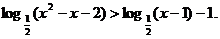
18.已知函数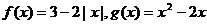 ,构造函数F(x),定义如下:当
,构造函数F(x),定义如下:当 时,
时,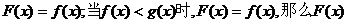 ( )
( )
A.有最大值3,最小值-1 B.有最大值3,无最小值
C.有最大值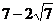 ,无最小值 D.无最大值,也无最小值
,无最小值 D.无最大值,也无最小值
17.若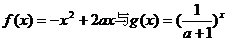 在区间[1,2]上都是减函数,则a的取值范围是
在区间[1,2]上都是减函数,则a的取值范围是
( )
A.(-1,0) B.(-1,1)
C.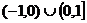 D.
D.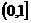
16.函数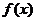 是奇函数,当
是奇函数,当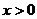 时,
时,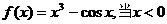 时,
时,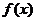 的表达式( )
的表达式( )
A.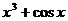 B.
B.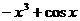
C.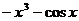 D.
D.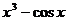
15.“函数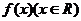 存在反函数”是“函数
存在反函数”是“函数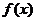 在R上的单调函数”的 ( )
在R上的单调函数”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com