
8.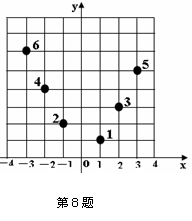 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列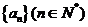 的前12项,如下表所示:
的前12项,如下表所示:

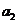
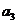
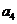
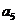
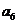
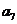
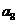
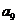
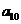

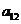
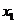
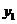

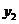

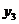
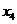
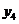
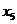
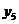
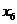
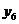
按如此规律下去,则 ( )
( )
A.1003 B.1005 C.1006 D.2011
7.2009年浙江省新课程自选模块考试试卷中共有18道试题,要求考生从中选取6道题进
行解答,其中考生甲第2,6,9,13,14,17,18题一定不选,考生乙第7,9,13,14,
17,18题一定不选,且考生甲与乙选取的6道题没有一题是相同的,则满足条件的选法种
数共有 ( )
A.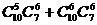 B.
B.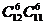 C.
C.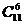 D.
D.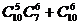
6.将函数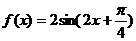 的图象向右平移(
的图象向右平移(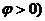 个单位,再将图象上每一点的横坐标缩短到原来的
个单位,再将图象上每一点的横坐标缩短到原来的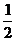 倍,所得图象关于直线
倍,所得图象关于直线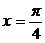 对称,则的最小正值为 ( )
对称,则的最小正值为 ( )
A. 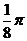 B.
B. 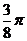 C.
C. 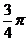 D.
D. 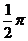
5.已知命题“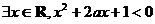 ”是真命题,则实数a的取值范围是 ( )
”是真命题,则实数a的取值范围是 ( )
A.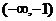 B.
B.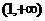 C.
C.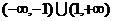 D.(-1,1)
D.(-1,1)
4.在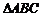 中,角A,B所对的边长为
中,角A,B所对的边长为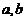 ,则“
,则“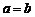 ”是“
”是“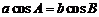 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
3.若二项式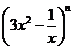 的展开式中各项系数的和是512,则展开式中的常数项为
( )
的展开式中各项系数的和是512,则展开式中的常数项为
( )
A.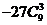 B.
B.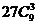 C.
C.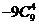 D.9
D.9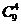
2.在空间中,两条不同的直线m、n,两个不同的平面、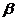 ,则下列命题中的真命题是( )
,则下列命题中的真命题是( )
A.若⊥,n⊥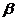 ,⊥
,⊥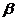 ,则m⊥n B.若m⊥,n∥
,则m⊥n B.若m⊥,n∥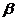 ,⊥
,⊥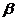 ,则m⊥n
,则m⊥n
C.若m∥,n∥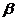 ,∥
,∥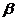 ,则m∥n D.若m∥,n⊥
,则m∥n D.若m∥,n⊥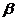 ,⊥
,⊥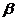 ,则m∥n
,则m∥n
只有一项是符合题目要求的。
1.命题“ ”的否定为
( )
”的否定为
( )
A. 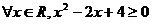 B.
B. 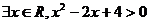
C. 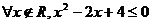 D.
D.
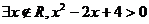
22. (本小题满分15分)设函数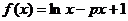
(Ⅰ)求函数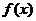 的单调区间;
的单调区间;
(Ⅱ)当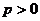 时,若对任意的
时,若对任意的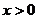 ,恒有
,恒有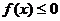 ,求的取值范围;
,求的取值范围;
(Ⅲ)证明: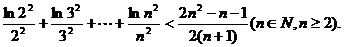
嘉兴市第一中学2009学年第一学期12月月考
19. (本题满分14分)已知等差数列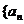 }的公差
}的公差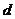 大于0,且
大于0,且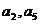 是方程
是方程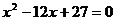 的两根,数列
的两根,数列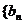 }的前项和为
}的前项和为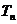 ,且
,且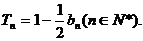
(Ⅰ)求数列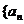 }、
}、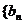 }的通项公式;
}的通项公式;
(Ⅱ)记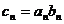 ,求数列
,求数列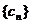 中的最大项.
中的最大项.
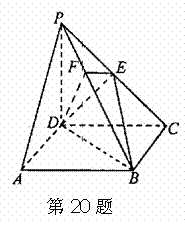 20. (本题满分14分)如图,在四棱锥
20. (本题满分14分)如图,在四棱锥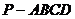 中,底面
中,底面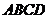
是正方形,侧棱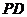 ⊥底面
⊥底面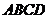 ,
,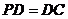 .点是
.点是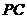 的中点,
的中点,
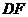 ⊥
⊥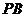 ,且交
,且交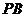 于点.
于点.
(Ⅰ)证明: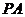 ∥平面
∥平面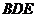 ;
;
(Ⅱ)证明: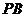 ⊥平面
⊥平面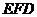 ;
;
(Ⅲ)求二面角 的大小.
的大小.
.21. (本小题满分15分) 已知椭圆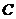 的中心在坐标原点,焦点在轴上,它的一个顶点
的中心在坐标原点,焦点在轴上,它的一个顶点
恰好是抛物线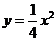 的焦点,离心率为
的焦点,离心率为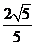
(Ⅰ)求椭圆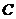 的标准方程;
的标准方程;
(Ⅱ)过椭圆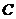 的右焦点作直线
的右焦点作直线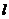 交椭圆
交椭圆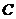 于、两点,交轴于
于、两点,交轴于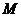 点,若
点,若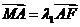 ,
,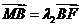 ,求
,求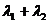 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com