
1. 代数推理
由于二次函数的解析式简捷明了,易于变形(一般式、顶点式、零点式等),所以,在解决二次函数的问题时,常常借助其解析式,通过纯代数推理,进而导出二次函数的有关性质.
22.(理)解:(1)由条件,得 ,------------------1分
,------------------1分
当 时,总有
时,总有 ,所以有
,所以有
|

由①+②得, ,
,
又b≥-2,∴b=-2,---------------------------------------------------------------------------4分
把b=-2代入①和②得
 因此
因此 --------------------7分
--------------------7分
(2) ,
,
 是关于x的二次函数,--------------------------------------------8分
是关于x的二次函数,--------------------------------------------8分
当 时,
时, 或
或
 或
或 -------------------------------11分
-------------------------------11分
解得, . 因此,当
. 因此,当 时,
时, 的恒成立,则
的恒成立,则 -------12分
-------12分
由 >0(0≤x≤1)可知,当1≤m≤
>0(0≤x≤1)可知,当1≤m≤ 时g(x)在[0,
时g(x)在[0,  ]为增函数,在[
]为增函数,在[ ,1]上为减函数|,|g(0)|=3≤3.5,|g(1)|=|m-4|≤3,|g(
,1]上为减函数|,|g(0)|=3≤3.5,|g(1)|=|m-4|≤3,|g( )|=|
)|=| |≤3.5,即|g(x)|≤3.5;-------------------------------------------------------13分
|≤3.5,即|g(x)|≤3.5;-------------------------------------------------------13分
当 ≤m≤
≤m≤ 时g(x)在[0,1]为增函数,|g(0)|=3≤3.5,|g(1)|=|m-4|≤2.5,即|g(x)|≤3.5。综上所述,当
时g(x)在[0,1]为增函数,|g(0)|=3≤3.5,|g(1)|=|m-4|≤2.5,即|g(x)|≤3.5。综上所述,当 时,若
时,若 恒成立,则|g(x)|≤3.5也恒成立.--------14分
恒成立,则|g(x)|≤3.5也恒成立.--------14分
22(文)(I)三个函数的最小值一次为: ,由
,由 得
得 ,所以,
,所以, ,故方程
,故方程 的两根为
的两根为
 ,由韦达定理消去得
,由韦达定理消去得
(II)① ; ②
; ②
由(I)知
 的取值范围为
的取值范围为

20.解(Ⅰ)设等差数列 的公差为
的公差为 ,
, ,因为
,因为 ,则
,则
 ,即
,即 . (2分)
. (2分)
整理得, .
(3分)
.
(3分)
因为对任意正整数上式恒成立,则 ,解得
,解得 . (5分)
. (5分)
故数列 的通项公式是
的通项公式是 .
(6分)
.
(6分)
(Ⅱ)由已知,当 时,
时, .因为
.因为 ,所以
,所以 .
(7分)
.
(7分)
当 时,
时, ,
, .
.
两式相减,得 .
.
因为 ,所以
,所以 =
= .
(9分)
.
(9分)
显然 适合上式,所以当
适合上式,所以当 时,
时, .
.
于是 .
.
因为 ,则
,则 ,所以数列
,所以数列 是首项为1,公差为1的等差数列.(12分)
是首项为1,公差为1的等差数列.(12分)
所以 不为常数,故数列
不为常数,故数列 不是“科比数列”.
(13分)
不是“科比数列”.
(13分)
21解:(1)数列的通项为 .故
.故 ,易知,
,易知, .
.
(2)假设存在实数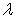 ,使得当
,使得当 时,
时,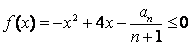 对任意
对任意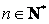 恒成立,则
恒成立,则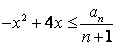 对任意
对任意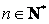 都成立,,
都成立,,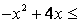
 ,
,
得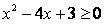 ,有
,有 或
或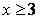 .故存在最大的实数
.故存在最大的实数 符合题意.
符合题意.
19. 解:(1)该四棱锥相应的俯视图为内含对角线、边长为6cm的正方形(如下图)----2分
解:(1)该四棱锥相应的俯视图为内含对角线、边长为6cm的正方形(如下图)----2分
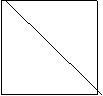 其面积为:6×6=36(cm2)---4分
其面积为:6×6=36(cm2)---4分
(2)如图,以C为原点,CD为x
|
∴ ----7分
----7分
设平面LMN的法向量为 =(x,y,z)
=(x,y,z)
由 得
得 令x=2 则
令x=2 则 =(2,0,3)------------9分
=(2,0,3)------------9分
设 ,----------------------------------10分
,----------------------------------10分
则 -------------11分
-------------11分
由 ,得
,得 ,即
,即 =
= -------------------------------12分
-------------------------------12分
又EF 所以,EF//平面LMN------------------------------------13分
所以,EF//平面LMN------------------------------------13分
即在底面正方形的对角线AC上存在符合题意的点F,CF= AC=
AC= cm---------14分
cm---------14分
18.解(Ⅰ)设奖励函数模型为y=f(x),则公司对函数模型的基本要求是:
当x∈[10,1000]时,①f(x)是增函数;②f(x)≤9恒成立;③ 恒成立. (3分)
恒成立. (3分)
(Ⅱ)(1)对于函数模型 :
:
当x∈[10,1000]时,f(x)是增函数,则 .
.
所以f(x)≤9恒成立. (5分)
因为函数 在[10,1000]上是减函数,所以
在[10,1000]上是减函数,所以 .
.
从而 ,即
,即 不恒成立.
不恒成立.
故该函数模型不符合公司要求. (8分)
(2)对于函数模型f(x)=4lgx-3:
当x∈[10,1000]时,f(x)是增函数,则 .
.
所以f(x)≤9恒成立. (10分)
设g(x)=4lgx-3- ,则
,则 .
.
当x≥10时, ,所以g(x)在[10,1000]上是减函数,从而g(x)≤g(10)=-1<0.所以4lgx-3-
,所以g(x)在[10,1000]上是减函数,从而g(x)≤g(10)=-1<0.所以4lgx-3- <0,即4lgx-3<
<0,即4lgx-3< ,所以
,所以 恒成立,故该函数模型符合公司要求.
恒成立,故该函数模型符合公司要求.
17.解(Ⅰ)因为a·b=
 .
(2分)
.
(2分)
由 ,得
,得 ,即
,即 ,k∈Z.
,k∈Z.
所以f(x)的定义域是 .
(4分)
.
(4分)
因为 ,则
,则 ,
,
所以f(x)的值域是 .
(6分)
.
(6分)
(Ⅱ)由题设 .
.
若f(x)为增函数,则 为减函数,所以
为减函数,所以 ,即
,即
 ,故f(x)的递增区间是
,故f(x)的递增区间是 (9分)
(9分)
若f(x)为减函数,则 为增函数,所以
为增函数,所以 ,即
,即
 ,故f(x)的递减区间是
,故f(x)的递减区间是 .(12分)
.(12分)
13. 6 14.4 15.30 16. ② ④
1.A 2.B 3.C4. B 5.D6. B7.C 8..B 9.A 10. A 11.A 12.C
[解析]很多同学根据题意发现n=16可行,判除A,B选项,但对于C,D选项则难以作出选择,事实上,这是一道运筹问题,需要用函数的最值加以解决.设 的件数为
的件数为 (规定:当
(规定:当 时,则B调整了
时,则B调整了 件给A,下同!),
件给A,下同!),
 的件数为
的件数为 ,
,
 的件数为
的件数为 ,
, 的件数为
的件数为 ,依题意可得
,依题意可得 ,
, ,
, ,
, ,从而
,从而 ,
, ,
, ,故调动件次
,故调动件次 ,画出图像(或绝对值的几何意义)可得最小值为16,故选(C).
,画出图像(或绝对值的几何意义)可得最小值为16,故选(C).
22.(本小题满分12分) 已知函数 当
当 时,总有
时,总有 .
.
(I)求函数f(x)的解析式;(II)设函数 ,求证:当
,求证:当 时,若
时,若 恒成立,则|g(x)|≤3.5也恒成立.
恒成立,则|g(x)|≤3.5也恒成立.
21.(本小题满分12分)
定义 的“倒平均数”为
的“倒平均数”为 ,已知数列
,已知数列 前项的“倒平均数”为
前项的“倒平均数”为 .
.
(I)记 ,试比较
,试比较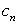 与
与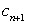 的大小;
的大小;
(II)是否存在实数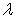 ,使得当
,使得当 时,
时, 对任意
对任意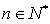 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数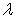 ;若不存在,说明理由.
;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com