
17.(2008年东北三省三校高三第一次联合模拟考试)已知向量
(1)当 时,求
时,求 的值;
的值;
(2)求 在
在 上的值域.
上的值域.
解(1) ,∴
,∴ ,∴
,∴
 (5分)
(5分)
(2)

∵ ,∴
,∴ ,∴
,∴
∴ ∴函数
∴函数  (10分)
(10分)
16.(2009玉溪一中期末)设函数
(Ⅰ)若 ,求x;
,求x;
(Ⅱ)若函数 平移后得到函数
平移后得到函数 的图像,求实数m,n的值。
的图像,求实数m,n的值。
解 (1)

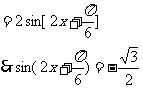
又



(2) 平移后
平移后
为 而
而

15.(2009牟定一中期中)已知: ,
, (
( ).
).
(Ⅰ) 求 关于
关于 的表达式,并求
的表达式,并求 的最小正周期;
的最小正周期;
(Ⅱ) 若 时,
时, 的最小值为5,求
的最小值为5,求 的值.
的值.
解 (Ⅰ)  ……2分
……2分

 .
.
 的最小正周期是
的最小正周期是 .
.
(Ⅱ) ∵ ,∴
,∴ .
.
∴当 即
即 时,函数
时,函数 取得最小值是
取得最小值是 .
.
∵ ,∴
,∴ .
.
14.(山东省乐陵一中2009届高三考前回扣45分钟练习三)已知向量m=( ,1),
,1),
n=( ,
,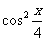 )。
)。
(1)若m•n=1,求 的值;
的值;
(2)记f(x)=m•n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足
(2a-c)cosB=bcosC,求函数f(A)的取值范围。
解 (I)m•n=
=
=
∵m•n=1
∴

=

(II)∵(2a-c)cosB=bcosC
由正弦定理得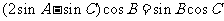
∴
∴
∵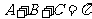
∴ ,且
,且
∴
∴
∴
又∵f(x)=m•n= ,
,
∴f(A)=
故函数f(A)的取值范围是(1, )
)
13.(2009丹阳高级中学一模)已知平面上的向量 、
、 满足
满足 ,
, ,设向量
,设向量 ,则
,则 的最小值是
的最小值是
答案 2
12.(2009扬州大学附中3月月考)在直角坐标系 中,
中, 分别是与
分别是与 轴,
轴,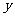 轴平行的单位向量,若直角三角形
轴平行的单位向量,若直角三角形 中,
中, ,
, ,则实数m= .
,则实数m= .
答案 -2或0
11.(天门市2009届高三三月联考数学试题文)给出下列命题
① 非零向量 、
、 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为30°;
的夹角为30°;
②  ·
· >0是
>0是 、
、 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
③ 将函数y=|x-1|的图象按向量 =(-1,0)平移,得到的图像对应的函数为y=|x|;
=(-1,0)平移,得到的图像对应的函数为y=|x|;
④若( )·(
)·( )=0,则△ABC为等腰三角形
)=0,则△ABC为等腰三角形
以上命题正确的是 。(注:把你认为正确的命题的序号都填上)
答案 ①③④
10.(2009上海九校联考)若向量 ,则向量
,则向量 的夹角等于
的夹角等于
答案 
9.(2009冠龙高级中学3月月考)若向量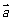 与
与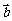 的夹角为
的夹角为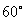 ,
, ,则
,则 _________.
_________.
答案 
8.(2009云南师大附中)设向量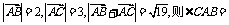 _________
_________
答案

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com