
1、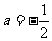 ;2、C;3、
;2、C;3、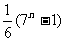 ;4、D
;4、D
[例题探究]
例1.(1)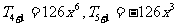 (2)有理项分别为:
(2)有理项分别为: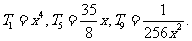
[教学建议] 要让学生来分析、解决问题,掌握用二项展开式的通项来处理问题,在教学中,要提醒学生二项式系数与某项系数的区别。
例2.15.[教学建议]让学生来分析展开式中每一项的由来,进而分析出常数项的由来。
例3.(1)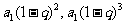 ;(2)
;(2)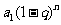 ;(3)
;(3)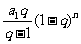
[教学建议]让学生来计算、归纳、总结,利用等比数列基本量的关系,熟悉二项式定理,将所求问题凑成二项式定理的形式。
(备用题)方法一、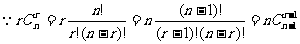
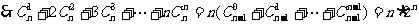
所以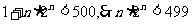
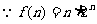 在
在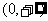 递增
递增
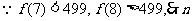 的最大值为7。
的最大值为7。
方法二、利用倒序相加法求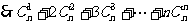 ,以下同上。
,以下同上。
[教学建议]:本题的教学,首先要求学生找出通项,化简通项,找出规律,利用二项式系数性质求和或观察机构特点利用调头相加求和;充分利用单调性解不等式。
冲刺强化训练(25)
8.设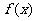 是定义在
是定义在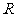 上的函数,且
上的函数,且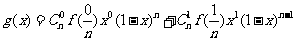

(1)若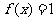 ,求
,求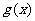 ;
;
(2)若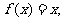 求
求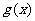 。
。
第25讲 二项式定理的应用
[考前热身]
7.若某一等差数列的首项为 ,公差为
,公差为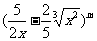 展开式的常数项,其中
展开式的常数项,其中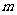 是
是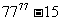 除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
6.若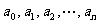 是一个等差数列,公差为
是一个等差数列,公差为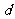 ,试求
,试求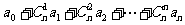 的值。
的值。
5.关于二项式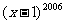 有下列四个命题,其中正确的序号是
有下列四个命题,其中正确的序号是
(1)该二项展开式中非常数项的系数和是1;
(2)该二项展开式系数最大的项是第1004项;
(3)该二项展开式中第六项为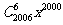 ;
;
(4)当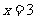 时,
时,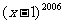 除以7的余数是4。
除以7的余数是4。
4.(1)设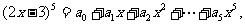 则
则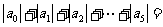
(2)设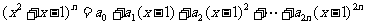 ,则
,则
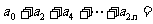 ,
,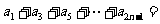
3.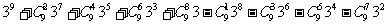 =
=
2、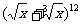 的展开式中,含x的正整数次幂的项共有( )
的展开式中,含x的正整数次幂的项共有( )
A.4项 B.3项 C.2项 D.1项
1.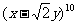 的展开式中
的展开式中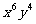 项的系数是( )
项的系数是( )
A.840 B.-840 C.210 D.-210
2、二项式定理的应用不仅要注重它的“正用”,而且重视它的“逆用”比如例3 及备选题。
冲刺强化训练(24)
班级_____ 姓名_____ 学号_____ 日期__月__日
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com