
19.已知函数f (x) = x – ln (x + a)在x = 1处取得极值.
(1)求实数a的值;
(2)若关于x的方程f (x) + 2x = x2 + b在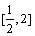 上恰有两个不相等的实数根,求实数b的取值范围
上恰有两个不相等的实数根,求实数b的取值范围
[解析](1)对f
(x)求导,得f′(x) = 1 – 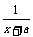 .
.
由题意,得f′(1)
= 0,即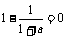 ,∴a
= 0.
,∴a
= 0.
(2)由(1)得f (x) = x – ln x,∴f (x) + 2x = x2 + b,即x2 – 3x + lnx + b = 0.
设g
(x) = x2 – 3x + lnx + b
(x>0),则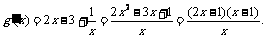
令g′(x) = 0,得x1 =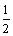 ,x2 = 1.
,x2 = 1.
当x变化时,g′(x)、g (x)的变化情况如下表:
|
x |
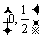 |
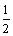 |
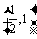 |
1 |
(1,2) |
2 |
|
g′(x) |
+ |
0 |
– |
0 |
+ |
+ |
|
g (x) |
 |
极大值 |
 |
极小值 |
 |
b – 2 + ln2 |
∴当x = 1时,g (x)的极小值为g (1) = b – 2.
又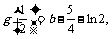 g (2) = b
– 2 + ln2.
g (2) = b
– 2 + ln2.
∵方程f
(x) + 2x = x2 + b 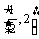 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,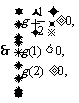
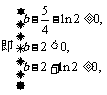 解得
解得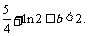
18.(本小题满分13分)
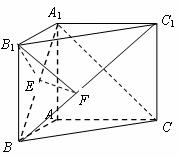
在直三棱柱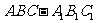 中,
中,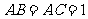 ,
,
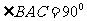 ,且异面直线
,且异面直线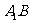 与
与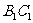 所成
所成
的角等于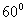 ,设
,设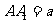 .
.
(Ⅰ)求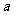 的值;
的值;
(Ⅱ)求平面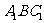 与平面
与平面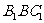 所成的锐二面角的大小.
所成的锐二面角的大小.
解法一:(1)建立如图坐标系,于是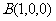 ,
,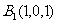 ,
,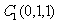 ,
,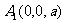 (
( )
)
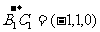 ,
,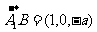 ,
,
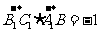
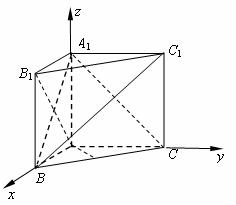 由于异面直线
由于异面直线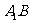 与
与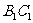 所成的角
所成的角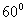 ,
,
所以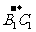 与
与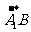 的夹角为
的夹角为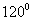
即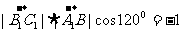
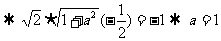
(2)设向量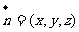 且
且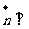 平面
平面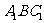
于是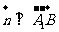 且
且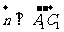 ,即
,即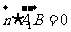 且
且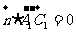 ,
,
又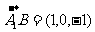 ,
,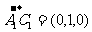 ,所以
,所以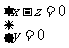 ,
,
不妨设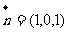 同理得
同理得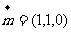 ,使
,使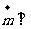 平面
平面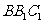 ,
,
设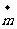 与
与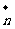 的夹角为
的夹角为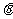 ,所以依
,所以依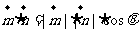 ,
,
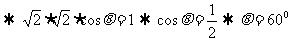 ,
,
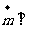 平面
平面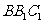 ,
, 平面
平面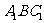 ,
,
因此平面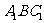 与平面
与平面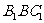 所成的锐二面角的大小为
所成的锐二面角的大小为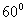 。
。
说明:或者取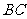 的中点
的中点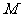 ,连接
,连接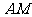 ,
,
于是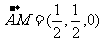 显然
显然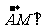 平面
平面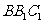
解法二:(1)
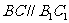 ,
,
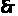
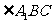 就是异面直线
就是异面直线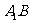 与
与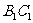 所成的角,
所成的角,
即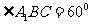 ,
,
连接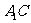 ,又
,又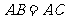 ,则
,则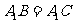
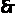
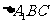 为等边三角形,由
为等边三角形,由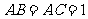 ,
,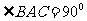
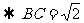 ,
,
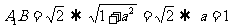 ;
;
(2)取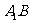 的中点
的中点 ,连接
,连接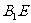 ,过
,过 作
作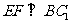 于
于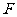 ,
,
连接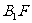 ,
,
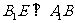 ,
,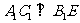
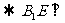 平面
平面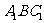
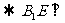
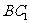
又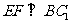 ,所以
,所以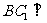 平面
平面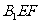 ,即
,即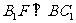 ,
,
所以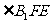 就是平面
就是平面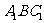 与平面
与平面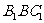 所成的锐二面角的平面角。
所成的锐二面角的平面角。
在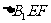 中,
中,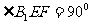 ,
,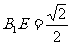 ,
,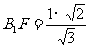 ,
,
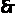
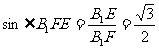
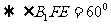 ,
,
因此平面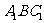 与平面
与平面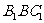 所成的锐二面角的大小为
所成的锐二面角的大小为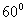 。
。
17.(本小题共13分)甲、乙两个射手进行射击训练,甲击中目标的概率为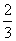 ,乙击中目标的概率为
,乙击中目标的概率为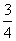 ,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”.(1)求一个“单位射击组”为“单位进步组”的概率;
,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”.(1)求一个“单位射击组”为“单位进步组”的概率;
(2)记完成三个“单位射击组”后出现“单位进步组”的次数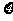 ,求
,求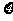 的分布列与数学期望.
的分布列与数学期望.
解:(1)设甲击中目标2次时为“单位进步组”的概率为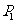 ,
,
则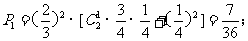
设甲击中目标1次时为“单位进步组”的概率为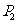 ,
,
则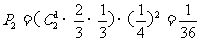 .
.
故一个“单位射击组”成为“单位进步组”的概率为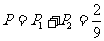 .
.
(2)由(1)知,一个“单位射击组”成为“单位进步组”的概率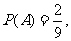 不能成为“单位进步组”的概率
不能成为“单位进步组”的概率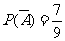 .
.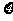 可能取值为0,1,2,3.
可能取值为0,1,2,3.
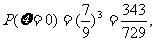
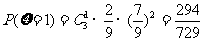
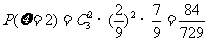 ,
,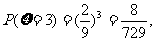
∴ 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
 |
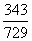 |
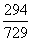 |
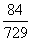 |
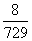 |
∴ 的数学期望
的数学期望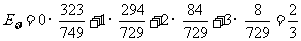 .
.
(或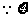 ﹀
﹀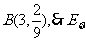
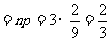 )
)
16、(本小题满分13分)
已知函数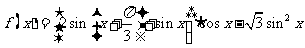
(1)若函数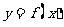 的图象关于直线
的图象关于直线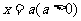 对称,求
对称,求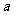 的最小值;
的最小值;
(2)若对任意的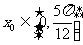 ,使得
,使得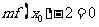 成立,求实数
成立,求实数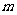 的取值范围。
的取值范围。
 =
=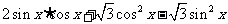
=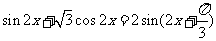
由题设可知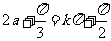 ,即
,即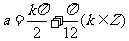 ,∵
,∵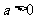 ,∴当
,∴当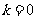 ,
,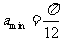
(2)当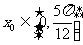 时,
时,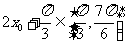 ,
,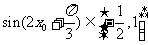 ,∴
,∴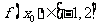
由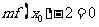 ,得
,得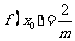 ,∴
,∴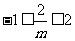 ,即
,即 或
或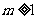
即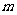 的取值范围是:
的取值范围是: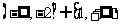
15.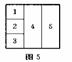 如图5,用4种不同的颜色对图中5个区域涂色(4种颜色全部使用),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色种数有 96
如图5,用4种不同的颜色对图中5个区域涂色(4种颜色全部使用),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色种数有 96
14.C;③④说法正确,①中应把“或”改成“且”,②中球面距离应是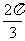
14.下列四种说法:
①命题“若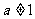 或
或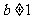 ,则
,则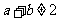 ”的否命题是“若
”的否命题是“若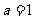 或
或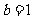 ,则
,则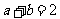 ”;
”;
②四面体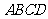 的外接球球心在棱
的外接球球心在棱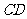 上,且
上,且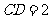 ,
,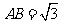 ,则在外接球球面上
,则在外接球球面上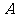 、
、 两点间的球面距离是
两点间的球面距离是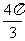 ;
;
③若函数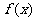 是R上的偶函数且对任意
是R上的偶函数且对任意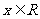 ,都有
,都有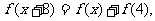 且
且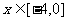 时,
时,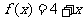 ,则
,则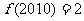
④在某项测量中,测量结果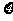 服从正态分布
服从正态分布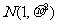 (
( ).若
).若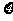 在
在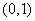 内取值的概率为0.4,则
内取值的概率为0.4,则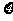 在
在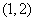 内取值的概率为0.4;
内取值的概率为0.4;
(5)抛物线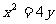 的准线与圆
的准线与圆 相交的弦长为2
相交的弦长为2
其中说法正确的有 ③④ 。 (填正确的序号) ( )
13.函数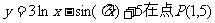 处的切线方程为
。
处的切线方程为
。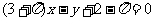
12.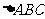 中,
中,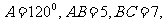 则
则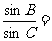 。
。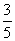
11.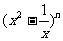 的展开式中,常数项为15,则(n=6)则展开式中二项式最大的项是 -20
的展开式中,常数项为15,则(n=6)则展开式中二项式最大的项是 -20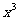 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com