
19、已知函数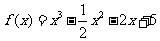
(Ⅰ)求函数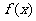 的单调区间;
的单调区间;
(Ⅱ)求函数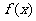 在区间[-1,2]上的最大值和最小值.
在区间[-1,2]上的最大值和最小值.
解:(Ⅰ)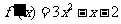 由
由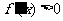 得
得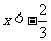 或
或 ,
,
故函数的单调递增区间为(-∞,-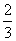 )和(1,+∞);由
)和(1,+∞);由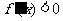 得
得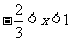 故函数的单调递减区间为(
故函数的单调递减区间为(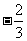 ,1)(也可以用闭区间的形式) (6分)
,1)(也可以用闭区间的形式) (6分)
(Ⅱ)由(1)知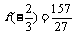 是函数的极大值,
是函数的极大值,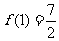 是函数的极小值;
是函数的极小值;
而区间[-1,2]端点的函数值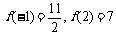
故在区间[-1,2]上函数的最大值为7,最小值为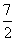 (12分)
(12分)
18、解不等式: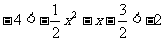
解: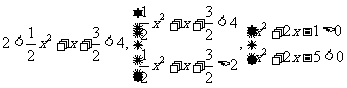
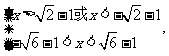
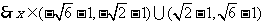
17、已知集合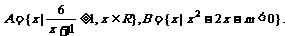
(1)当 =3时,求
=3时,求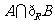 ;
;
(2)若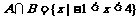 ,求实数
,求实数 的值.
的值.
解:由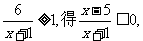
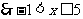
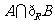
 ,………………2分
,………………2分
(Ⅰ)当m=3时,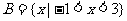 ,
,
则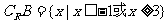 ……………………4分
……………………4分
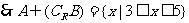 ………………6分
………………6分
(II)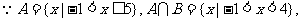 ………………8分
………………8分
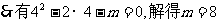 ,………………11分
,………………11分
此时 ,符合题意,故实数m的值为8.………………12分
,符合题意,故实数m的值为8.………………12分
16、设函数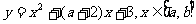 的图像关于直线
的图像关于直线 对称,则
对称,则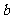 = 6__
= 6__
15、函数 是幂函数,且在
是幂函数,且在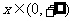 上是减函数,
上是减函数,
则实数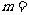 __2____
__2____
14、已知实数 的最大值为 1
的最大值为 1
13、已知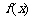 是
是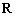 上的奇函数,当
上的奇函数,当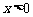 时,
时, ,则
,则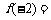 -1 .
-1 .
12、已知函数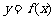 是偶函数,
是偶函数,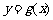 是奇函数,它们的定义域为
是奇函数,它们的定义域为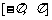 ,且它们
,且它们
在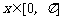 上的图象如下图所示,则不等式
上的图象如下图所示,则不等式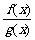 >0的解集为( B )
>0的解集为( B )
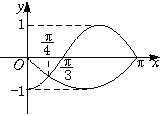 A.
A.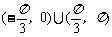 B.
B.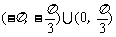
C.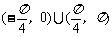 D.
D.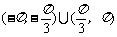
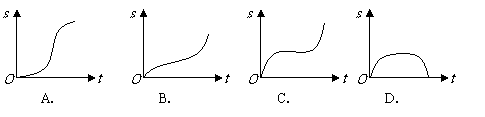
11、汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程 看作时间
看作时间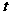 的函数,其图像可能是 ( A )
的函数,其图像可能是 ( A )
10、关于x的函数y=log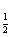 (x2-ax+2a)在[1,+∞
(x2-ax+2a)在[1,+∞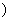 上为减函数,则实数a的
上为减函数,则实数a的
取值范围是( ) (-1,2]
A.( ,2] B.(
,2] B.(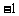 ,0) C.(0,2
,0) C.(0,2 D.(-∞,-1)
D.(-∞,-1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com