
21.设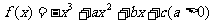 ,在
,在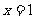 处取得极大值,且存在斜率为
处取得极大值,且存在斜率为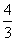 的切线。
的切线。
(1)求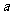 的取值范围;
的取值范围;
(2)若函数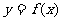 在区间
在区间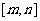 上单调递增,求
上单调递增,求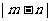 的取值范围;
的取值范围;
(3)是否存在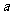 的取值使得对于任意
的取值使得对于任意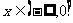 ,都有
,都有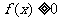 。
。
20.某商店投入38万元经销某种纪念品,经销时 人60天,为了获得更多的利润,商店将每天获得的利润投入到次日的经营中,市场调研表明,该商店在经销这一产品期间第 天的利润
天的利润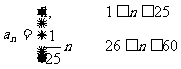 (单位:万元,
(单位:万元,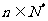 ),记第
),记第 天的利润率
天的利润率 ,例如
,例如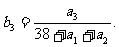
(1)求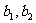 的值;
的值;
(2)求第 天的利润率
天的利润率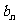 ;
;
(3)该商店在经销此纪品期间,哪一天的利润率最大?并求该天的利润率。
19.设A、B分别是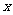 轴,
轴,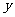 轴上的动点,P在直线AB上,且
轴上的动点,P在直线AB上,且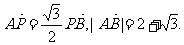
(1)求点P的轨迹E的方程;
(2)已知E上定点K(-2,0)及动点M、N满足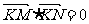 ,试证:直线MN必过
,试证:直线MN必过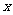 轴上的定点。
轴上的定点。
18.如图,在直角梯形ABCD中,AD//BC,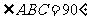 ,当E、F分别在线段AD、BC上,且
,当E、F分别在线段AD、BC上,且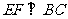 ,AD=3,BC=4,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=3,BC=4,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
(1)证明:直线AB与CD是异面直线;
(2)当直线AC与平面EFCD所成角为30°时,求二面角A-DC-E的余弦值。

17.2010年5月1日,上海世博会将举行,在安全保障方面,警方从武警训练基地挑选防爆警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选。假定某基地有4名武警战士(分别记为A、B、C、D)拟参加挑选,且每人能通过体能、射击、反应的概率分别为 。这三项测试能否通过相互之间没有影响。
。这三项测试能否通过相互之间没有影响。
(1)求A能够入选的概率;
(2)规定:每有1人入选,则相应的训练基地得到3000元的训练经费,否则得不到训练经费,求该基地得到训练经费恰为6000元的概率。
16.在 中,内角A、B、C所对的边分别为
中,内角A、B、C所对的边分别为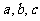 ,其外接圆半径为6,
,其外接圆半径为6,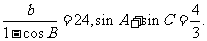
(1)求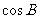 ;
;
(2)求 的面积的最大值。
的面积的最大值。
15.如图,在平面斜坐标系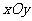 中,
中,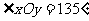 ,斜坐标定义:如果
,斜坐标定义:如果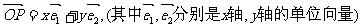 ,则(
,则( )叫做P的斜坐标。
)叫做P的斜坐标。
(1)已知P的斜坐标为 ,则
,则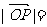 。
。 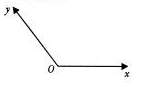
(2)在此坐标系内,已知A(0,2),B(2,0),动点P满足
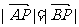 ,则P的轨迹方程是
。
,则P的轨迹方程是
。
14. 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高为35米,在地面上有一点A,测得A,C间的距离为91米,从A观测电视发射塔的视角
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高为35米,在地面上有一点A,测得A,C间的距离为91米,从A观测电视发射塔的视角
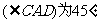 ,则这座电视发射塔的高度为
米。
,则这座电视发射塔的高度为
米。
13.当
 时,变量的取值范围是
。
时,变量的取值范围是
。
12.在抛物线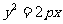 上,横坐标为4的点到焦点的距离为5,则
上,横坐标为4的点到焦点的距离为5,则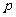 的值为
。
的值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com