
当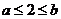 时,函数的最小值
时,函数的最小值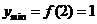 ,
,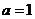 .
.
而函数的最大值应为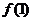 ,
,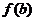 中的较大者,
中的较大者,
而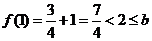 ,
,
故其最大值应为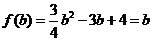
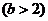 ,
,
解此方程得,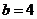 .
.
当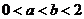 时,函数
时,函数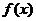 在区间
在区间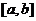 上单调减少.
上单调减少.
此时应有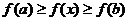 ,
,
即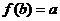 ,
,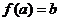 .
.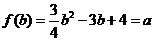 ,
, ,
,
解上述联立方程组,可得 ,不合题意.
,不合题意.
当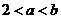 时,函数
时,函数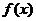 在区间
在区间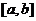 上单调增加.
上单调增加.
当
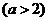 时,
时,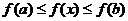 .
.
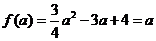 ,即
,即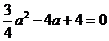 ,解得
,解得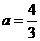 或
或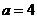 ;
;
同理解方程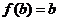 有
有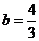 或
或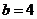 ,
,
则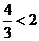 ,也不合题意.
,也不合题意.
综上所述知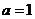 ,
,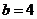 .
.
其函数值也恰有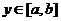 ,求常数
,求常数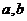 的值.
的值.
解方程组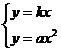 与
与 ,
,
求得两交点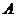 ,
,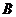 的坐标为
的坐标为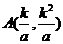 ,
,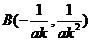 ,
,
设弦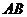 的中点
的中点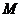 的坐标为
的坐标为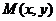 ,则有
,则有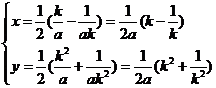 ,
,
∴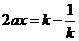 ,
,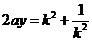 ,
,
即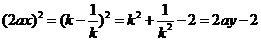 .
.
∴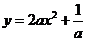 ,即点
,即点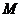 的轨迹方程为
的轨迹方程为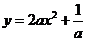 .
.
(2)∵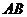 的斜率
的斜率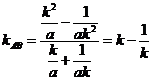 ,
,
∴过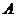 ,
,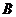 两点的直线方程为
两点的直线方程为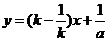 ,显然该直线恒过定点
,显然该直线恒过定点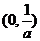 .
.
(3)∵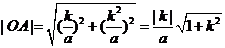 ,
,
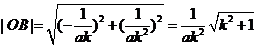 ,
,
∴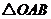 的面积
的面积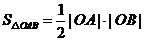
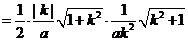
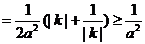 .
.
即当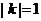
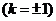 时,
时,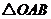 的面积取得最小值
的面积取得最小值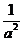 .
.
两点.
(1)求弦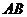 的中点
的中点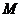 的轨迹方程;
的轨迹方程;
(2)证明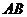 恒过一个定点,并求出这个定点的坐标;
恒过一个定点,并求出这个定点的坐标;
(3)求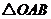 的面积的最小值.
的面积的最小值.
两式相减得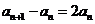 ,即
,即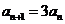
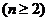 ,
,
又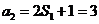 ,∴
,∴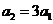 .
.
故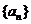 是首项为
是首项为 ,公比为
,公比为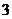 的等比数列,∴
的等比数列,∴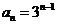 .
.
(2)设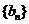 的公差为
的公差为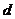 ,由
,由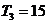 可得
可得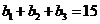 ,
,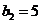 ,
,
故可设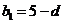 ,
,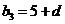 ,又
,又 ,
,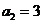 ,
,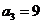 ,
,
由题意可得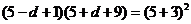 ,
,
解得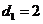 ,
,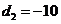 .
.
∵等差数列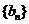 的各项为正,
的各项为正,
∴ ,
,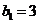 ,
,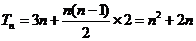 .
.
(1)求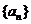 的通项公式;
的通项公式;
(2)等差数列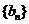 的各项为正,其前
的各项为正,其前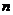 项和为
项和为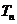 ,且
,且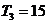 ,
,
又 ,
,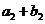 ,
,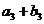 成等比数列,求
成等比数列,求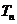 .
.
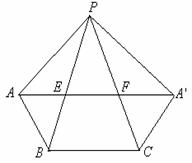
如图,连接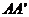 交
交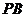 、
、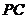 于
于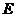 、
、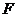 ,显然此时截面
,显然此时截面
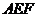 的周长最小;由
的周长最小;由 知
知
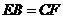 ,
,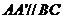 ,
,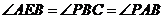 ,
,
所以,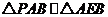 ,因
,因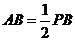 ,
,
知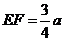 ,利用勾股定理,可求得等腰
,利用勾股定理,可求得等腰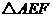
底边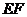 上的高的长度为
上的高的长度为
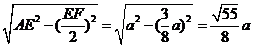 ,
,
故有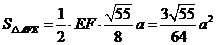 .
.
所求概率为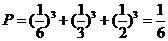 .
.
(2)这是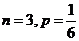 的独立重复实验,故所求概率为
的独立重复实验,故所求概率为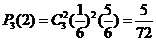 .
.
是打给甲、乙、丙的概率依次为 、
、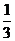 、
、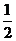 .若一段时间内打进三个电话,且各个电话相互独立.求:
.若一段时间内打进三个电话,且各个电话相互独立.求:
(1)这三个电话是打给同一个人的概率;
(2)这三个电话中恰有两个是打给甲的概率.
2.解:设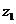 、
、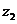 对应的向量
对应的向量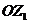 与
与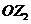 的夹角为
的夹角为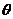 ,
,
由余弦定理得: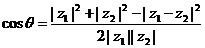
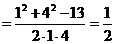 ,
,
∴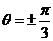 ,
,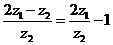
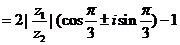
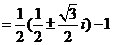
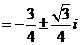 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com