
第一节 听力理解(5段共15小题;每小题2分,满分30分)
每段播放两遍。各段后有几个小题,各段播放前每小题有5秒钟的阅题时间。请根据各段播放内容及相关小题,在5秒钟内从题中所给的A、B、C项中,选出最佳选项,并在答题卡上将该项涂黑。
听第一段对话,回答第1-3题。
1. Where probably is the woman now?
A. In the Emergency Services.
B. In an elevator.
C. On the 15th floor of the Brill building.
2. What is the problem with the woman’s friend?
A. She has been bitten by a dog.
B. She is having difficulty in breathing.
C. She fell downstairs and was out.
3. What advice does the man give the woman?
A. She should keep her friend calm and far away from the dog.
B. She should leave her friend where she is.
C. She should send a rescue team and an ambulance right away.
听第二段对话,回答第4-6题。
4. How old is the man?
A. 78. B. 75. C. 72.
5. What do you learn from the conversation?
A. No streets of the city are more glorious than Sweet Jesus.
B. The woman is looking for her client’s office.
C. The woman is new to the city.
6. Where is the building?
A. It’s at No.149.
B. It’s on the left of Joe’s.
C. It’s three blocks away next to a baker’s.
听第三段对话,回答第7-9题。
7. How many home accidents involving children can be prevented every year in Britain?
A. About 10,000. B. About 900,000. C. About 1,000,000.
8. What do we learn about parents?
A. Parents should use mats to prevent children slipping on the floor of the bathroom.
B. Parents should keep the appliances, hot foods within reach.
C. Parents should accompany children all the time.
9. According to the woman, which is the most dangerous room in the house?
A. The bathroom. B. The kitchen. C. The living room.
听第四段对话,回答第10-12题。
10. When did the earthquake strike?
A. At midnight. B. At dawn. C. At dusk.
11. What do we know about the earthquake?
A. It was a mild one.
B. There was more than one aftershock.
C. There were no other survivors.
12. What happened to the apartment building?
A. It collapsed completely.
B. Half of the building was in ruins.
C. The first floor was totally flattened.
听第五段独白,回答第13-15题。
13. What is the talk mainly about?
A. The prize wars.
B. The entertainment awards.
C. The Grammy Awards, Golden Globes and People’s Choice Awards.
14. In some people’s opinion, what draws more attention in ceremonies?
A. What the winners say.
B. What the winners wear.
C. What the winners show.
15. What impresses the speaker most?
A. The pre-show.
B. The announcement of winners.
C. What the stars will say.
21.(本小题满分14分)
设 是关于
是关于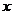 的方程
的方程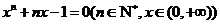 的根. 试证明:
的根. 试证明:
(1)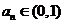 ;
;
(2)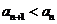 ;
;
(3)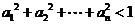 .
.
证明:(1)设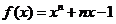 ,
,
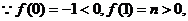 且函数
且函数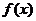 的图象在
的图象在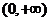 上是连续的,
上是连续的,
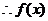 在
在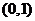 上至少有一个零点,即方程
上至少有一个零点,即方程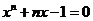 在
在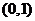 内至少有一个根.
内至少有一个根.
……………………………………………………………………… 3分
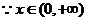 ,
,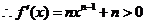 ,
,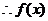 在
在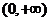 上是增函数.
上是增函数.
 方程
方程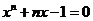 在
在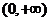 内有唯一根,且根在
内有唯一根,且根在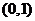 内,即
内,即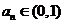 .…………
5分
.…………
5分
(2)方法一: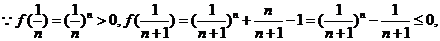
且函数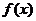 的图象在
的图象在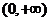 上是连续的,
上是连续的,
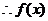 在
在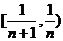 内至少有一个零点,即方程
内至少有一个零点,即方程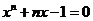 在
在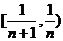 内至少有一个根.
内至少有一个根.
又由(1)知函数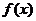 在
在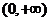 上单调递增,
上单调递增,
 方程
方程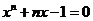 在
在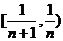 内有唯一根,
内有唯一根,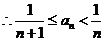 .……………………… 8分
.……………………… 8分
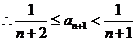 ,
, . …………………………………… 9分
. …………………………………… 9分
方法二:由(1)知,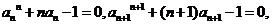 两式相减得:
两式相减得:
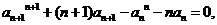 ………………………………………………7分
………………………………………………7分
若存在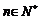 ,使得
,使得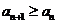 ,则
,则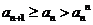 ,从而
,从而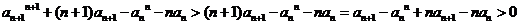 ,矛盾.
,矛盾.
所以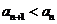 .
………………………………………………………… 9分
.
………………………………………………………… 9分
(3)由题设得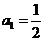 ,
,
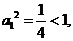
当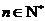 时,
时,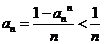 .
.
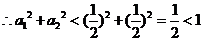 . ……………………………………12分
. ……………………………………12分
当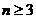 时有
时有

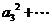
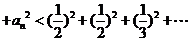
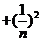
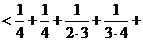 …
…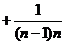


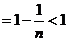 .
.
综上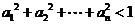 .
…………………………………………… 14分
.
…………………………………………… 14分
20.(本小题满分14分)
已知函数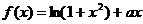 ,其中
,其中 为不大于零的常数.
为不大于零的常数.
(1) 讨论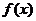 的单调性;
的单调性;
(2) 求证: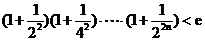 (
(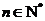 ,
,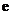 为自然对数的底数).
为自然对数的底数).
解:(1)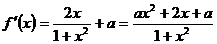 . ………………………………1分
. ………………………………1分
①当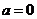 时,
时,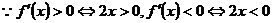 ,
,
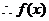 在
在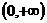 单调递增,在
单调递增,在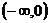 单调递减; ………………………………3分
单调递减; ………………………………3分
②当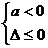 ,即
,即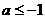 时,
时,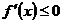 对
对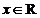 恒成立
恒成立
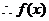 在
在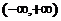 上单调递减; ……………………………………………… 5分
上单调递减; ……………………………………………… 5分
③当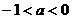 时,
时,
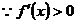
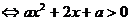
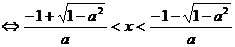
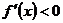

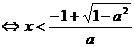 或
或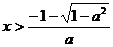
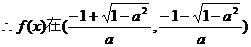 上单调递增,
上单调递增,
在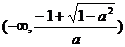 和
和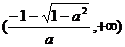 上单调递减; …………………… 7分
上单调递减; …………………… 7分
综上所述,当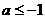 时,
时,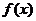 在
在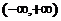 上单调递减,
上单调递减,
当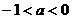 时,
时,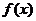 在
在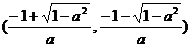 上单调递增,
上单调递增,
在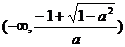 和
和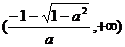 上单调递减.
上单调递减.
当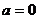 时,
时,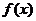 在
在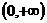 单调递增,在
单调递增,在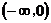 上单调递减. …………8分
上单调递减. …………8分
(2)由(1)知,当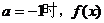 在
在 上单调递减,
上单调递减,
当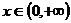 时,由
时,由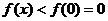 得
得
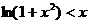 ……………………………10分
……………………………10分
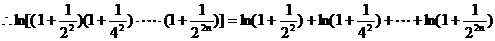
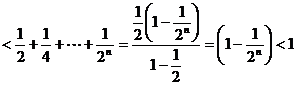
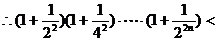
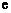 ………………………………………………14分
………………………………………………14分
19.(本小题满分14分)
如图,在直角梯形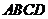 中,
中,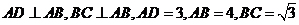 ,点
,点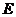 在线段
在线段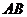 的延长线上.曲线段
的延长线上.曲线段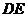 上任一点到
上任一点到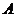 、
、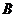 两点的距离之和都相等.
两点的距离之和都相等.
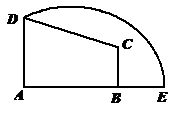 (1)建立适当的直角坐标系,求曲线段
(1)建立适当的直角坐标系,求曲线段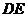 的方程;
的方程;
(2)试问:过点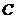 能否作一条直线
能否作一条直线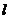 与曲线段
与曲线段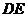 相交于两点
相交于两点
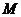 、
、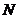 ,使得线段
,使得线段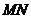 以C为中点?若能,则求直线
以C为中点?若能,则求直线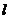
的方程;若不能,则说明理由.
 解:(1)以直线
解:(1)以直线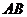 为
为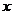 轴,线段
轴,线段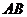 的中点为原点,
的中点为原点,
建立如图所示的平面直角坐标系,
则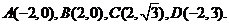 ……………… 1分
……………… 1分
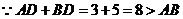 ,
,
 依题意,曲线段
依题意,曲线段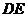 是以
是以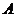 、
、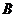 为左、右焦点,长轴长为
为左、右焦点,长轴长为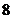 的椭圆的一部分. ………………………………………… 3分
的椭圆的一部分. ………………………………………… 3分
故曲线段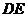 的方程为
的方程为 .
…………………………… 6分
.
…………………………… 6分
(2)设这样的直线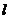 存在,由直线
存在,由直线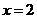 与曲线段
与曲线段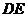 只有一个交点
只有一个交点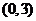 ,
,
知直线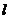 存在斜率,设直线
存在斜率,设直线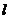 的方程为
的方程为 即
即
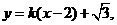
将其代入 得
得
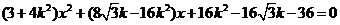 ① …………………… 9分
① …………………… 9分
设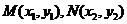 ,则由
,则由
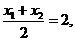 知
知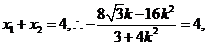 解得
解得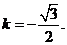 …………………12分
…………………12分
当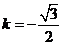 时,方程①化为:
时,方程①化为: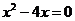 ,解得
,解得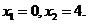
即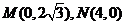 ,适合条件.
,适合条件.
故直线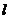 存在,其方程为
存在,其方程为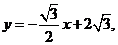 即
即 ……………… 14分
……………… 14分
18.(本小题满分14分)
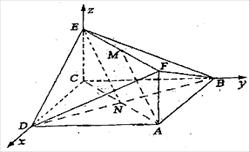
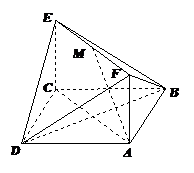 如图,已知正方形
如图,已知正方形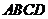 和矩形
和矩形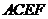 所在平面互相垂直,
所在平面互相垂直,
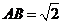 ,
,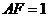 ,
,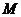 是线段
是线段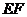 的中点.
的中点.
(1)求证: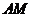 ∥平面
∥平面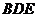 ;
;
(2)求二面角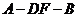 的大小;
的大小;
(3)试问:在线段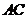 上是否存在一点
上是否存在一点 ,使得直线
,使得直线

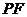 与
与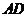 所成角为
所成角为 ?
?
解:方法一:(1)记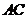 与
与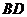 的交点为
的交点为 ,连接
,连接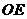 ,
,
∵ 、
、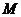 分别是
分别是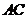 、
、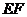 的中点,
的中点,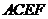 是矩形,
是矩形,
∴四边形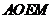 是平行四边形,∴
是平行四边形,∴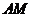 ∥
∥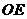 .
.
∵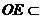 平面BDE,
平面BDE,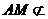 平面
平面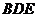 ,
,
∴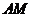 ∥平面
∥平面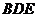 . ……………………………………………………………… 4分
. ……………………………………………………………… 4分
(2)在平面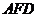 中过
中过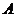 作
作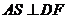 于
于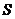 ,连结
,连结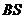 ,
,
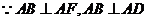 ,
, 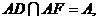 ∴
∴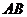 ⊥平面
⊥平面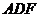 ,
,
∴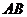 ⊥
⊥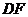 ,又
,又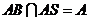
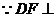 平面
平面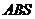
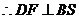 ,
,
∴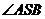 是二面角
是二面角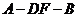 的平面角. ……………………………………… 6分
的平面角. ……………………………………… 6分
在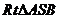 中,
中,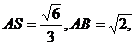 ∴
∴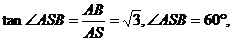
∴二面角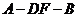 的大小为
的大小为 . ……………………………………………… 9分
. ……………………………………………… 9分
 (3)设
(3)设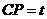 (
( ),作
),作 于Q,则
于Q,则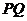 ∥
∥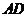 ,
,
∵ ,
,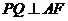 ,
,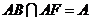 ,
,
∴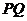 ⊥平面
⊥平面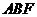 ,
,
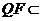 平面
平面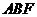 ,∴
,∴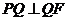 .
.
在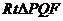 中,
中,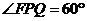 ,
,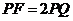 .
.
∵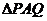 为等腰直角三角形,∴
为等腰直角三角形,∴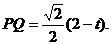
又∵Δ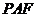 为直角三角形,∴
为直角三角形,∴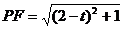 ,
,
∴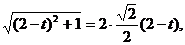
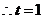 或
或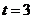 (舍去).
(舍去).
∴点 是
是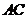 的中点. ……………………………………………………… 14分
的中点. ……………………………………………………… 14分
方法二:(1)建立如图所示的空间直角坐标系.设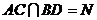 ,连接
,连接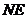 ,
,
则点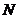 、
、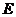 的坐标分别是(
的坐标分别是(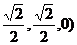 、
、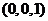 ,∴
,∴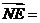 (
(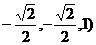 ,
,
又点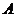 、
、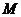 的坐标分别是(
的坐标分别是(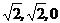 )、(
)、(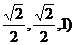 ,∴
,∴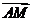 =(
=(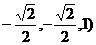
∴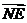 =
=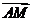 且
且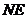 与
与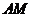 不共线,∴
不共线,∴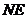 ∥
∥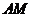 .
.
又∵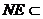 平面BDE,
平面BDE,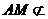 平面
平面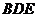 ,∴
,∴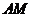 ∥平面
∥平面 . ………………… 4分
. ………………… 4分
 (2)
(2)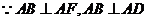 ,
,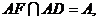 ∴
∴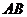 ⊥平面
⊥平面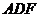 .
.
∴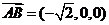 为平面
为平面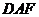 的法向量.
的法向量.
∵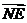
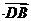 =(
=(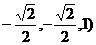 ·
·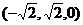 =0,
=0,
∴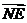 ·
·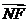 =(
=(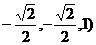 ·
·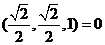 ,
,
得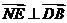 ,
,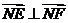 ∴
∴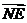 为平面
为平面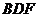 的法向量.
的法向量.
∴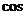 <
<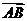 ,
,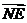 >
>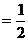 ,∴
,∴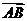 与
与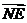 的夹角是
的夹角是 .
.
即所求二面角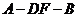 的大小是
的大小是 . ……………………………………………… 9分
. ……………………………………………… 9分
(3)设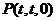
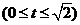 ,得
,得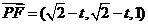 ,∴
,∴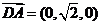 ,
,
又∵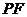 和
和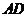 所成的角是
所成的角是 .
. 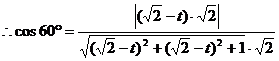 ,
,
解得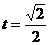 或
或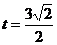 (舍去),即点
(舍去),即点 是
是 的中点. …………………………… 14分
的中点. …………………………… 14分
17.(本小题满分12分)
某休闲会馆拟举行“五一”庆祝活动,每位来宾交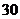 元的入场费,可参加一次抽奖活动. 抽奖活动规则是:从一个装有分值分别为
元的入场费,可参加一次抽奖活动. 抽奖活动规则是:从一个装有分值分别为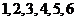 的六个相同小球的抽奖箱中,有放回的抽取两次,每次抽取一个球,规定:若抽得两球的分值之和为
的六个相同小球的抽奖箱中,有放回的抽取两次,每次抽取一个球,规定:若抽得两球的分值之和为 分,则获得价值为
分,则获得价值为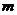 元的礼品;若抽得两球的分值之和为
元的礼品;若抽得两球的分值之和为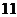 分或
分或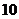 分,则获得价值为
分,则获得价值为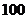 元的礼品;若抽得两球的分值之和低于
元的礼品;若抽得两球的分值之和低于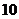 分,则不获奖.
分,则不获奖.
(1)求每位会员获奖的概率;
(2)假设这次活动会馆既不赔钱也不赚钱,则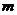 应为多少元?
应为多少元?
解:(1)两次抽取的球的分值构成的有序数对共有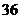 对,其中分值之和为
对,其中分值之和为 的有
的有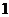 对,分值之和为
对,分值之和为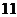 的有两对,分值之和为
的有两对,分值之和为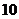 的有
的有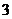 对,所以每位会员获奖的概率为
对,所以每位会员获奖的概率为
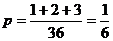 .
…………………………………………………………4分
.
…………………………………………………………4分
(2)设每位来宾抽奖后,休闲宾馆的获利的元数为随机变量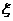 ,
,
则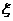 的可能取值为
的可能取值为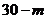 、
、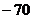 、
、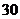 . ……………………………………………5分
. ……………………………………………5分

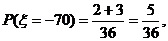
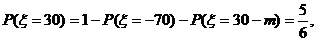 …………………………………8分
…………………………………8分
则宾馆获利的期望为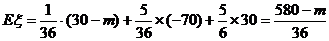 .
.
若这次活动会馆既不赔钱也不赚钱,则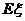 =0,即
=0,即 ,
,
所以,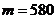 .
…………………………………………………………………………11分
.
…………………………………………………………………………11分
答:(1)每位会员获奖的概率为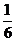 ;(2)
;(2)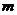 应为
应为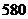 元.
…………………………12分
元.
…………………………12分
16.(本小题满分12分)
已知向量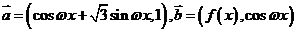 ,其中
,其中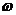 >0,且
>0,且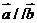 ,又函数
,又函数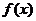 的图像两相邻对称轴之间的距离为
的图像两相邻对称轴之间的距离为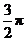 .
.
(1)求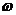 的值;
的值;
(2) 求函数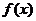 在区间
在区间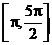 上的最大值与最小值及相应的
上的最大值与最小值及相应的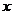 值.
值.
解:(1) 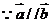 ,
,

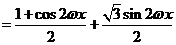
 .
.
……………………………………………… 4分
由题意,函数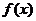 的最小正周期为
的最小正周期为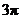 ,又
,又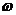 >0,
>0,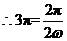
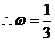 . ……………6分
. ……………6分
(2) 由(1)知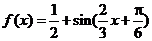 ,
,
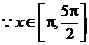 ,
,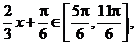
 当
当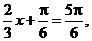 即
即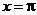 时,
时,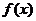 取得最大值
取得最大值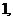 ……………………………… 9分
……………………………… 9分
当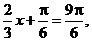 即
即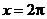 时,
时,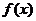 取得最小值
取得最小值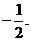 ………………………12分
………………………12分
9. 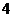 ; 10.
; 10.  ; 11.
; 11. 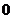 或
或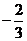 ;
12.
;
12. 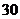 ; 13.
; 13.  ; 14.
; 14. 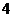 ; 15.
; 15. 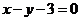 .
.
|
题次 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
答案 |
B |
C |
A |
C |
B |
C |
D |
D |
21.(本小题满分14分)
设 是关于
是关于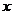 的方程
的方程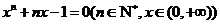 的根. 试证明:
的根. 试证明:
(1)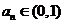 ;
;
(2)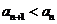 ;
;
(3)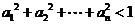 .
.
广东省2010届高三上学期四校联考
数 学(理科)
答案及说明
说明:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com