
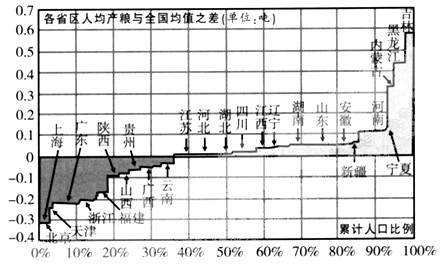
5. 福建省人均产粮状况的原因最不可能的是
A. 地形多山,可耕地比重小 B. 海拔较高,复种指数低
C. 农业结构调整,粮食种植面积下降 D. 工业化和城市化的发展,耕地面积减小
4. 该片林地的作用主要体现在
①涵养水源 ②保持水土 ③减弱噪声 ④吸烟滞尘 ⑤防风固沙
A. ①② B. ②⑤ C. ③④ D. ③⑤
读2006年我国粮食产出、人口份额的地域分布图,回答5-6题。
3. 探究结果表明
A. 学校所在地位于南半球 B. 林地的年温差大,裸地的年温差小
C. 该地7、8月份的月均温较低 D. 林地比裸地的年均气温低
2. 某游客购买的旅游纪念品中有一幅图示地区的航空照片,他发现教堂的日影大致朝向丁点
所在的方向。此航照的拍摄可能是当地时间
A.6月22 日 18:30 B. 12月22日 17:30
C.6月22日 5:30 D. 12月22日6:30
某中学地理探究性学习小组对该中学与高速公路之间的一片林地与裸地气温进行连续监测,测得林地与裸地月均温差值变化如下表。据此完成3-4题。
|
月 份 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
月均温差 值 |
0.13 |
0.10 |
0.18 |
-0.16 |
-0.13 |
-0.25 |
-0.43 |
-0.40 |
-0.20 |
-0.10 |
0.11 |
0.22 |
1. 甲、乙、丙、丁四地中可能有两条河汇流现象的地点和位于教堂西南方的地点分别是
A. 甲和丙 B. 乙和甲 C. 丙和甲 D. 丁和丙
21.(本小题满分12分)本小题主要考察直线、圆、椭圆、直线与圆锥曲线的位置关系等基本
 知识. 考察推理论证能力、运算求解能力,考察数形结合思想、化归与转化思想.
知识. 考察推理论证能力、运算求解能力,考察数形结合思想、化归与转化思想.
解:(Ⅰ)依题可得: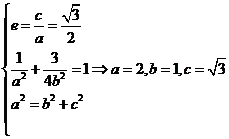
所以椭圆的方程为: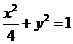 ………………………(4分)
………………………(4分)
(Ⅱ)由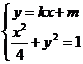 得
得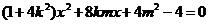


解得: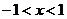 ………………………(7分)
………………………(7分)
(Ⅲ)存在 ………………………(8分)
理由如下:
方程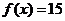 有且只有一个实根即为函数
有且只有一个实根即为函数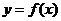 的图象与直线
的图象与直线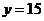 只有一
只有一
个公共点.
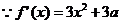
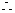 (1)若
(1)若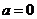 ,则
,则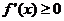 ,
,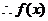 在实数集R上单调递增
在实数集R上单调递增
此时,函数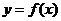 的图象与直线
的图象与直线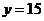 只有一个公共点. ………………(9分)
只有一个公共点. ………………(9分)
(2)若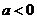 ,则
,则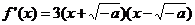 ………………………(10分)
………………………(10分)
列表如下:

20. (本小题满分12分)命题立意:本小题主要考查直线与直线、直线与平面、平面与平面
的位置关系等基础知识,考查了空间想象能力、推理论证能力和运算能力以及化归与转化
能力.
解:(Ⅰ)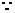 在
在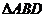 中,
中,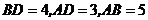
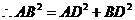
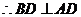 ………………………(2分)
………………………(2分)
又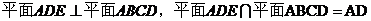
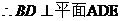
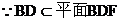

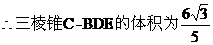 ………………………(12分)
………………………(12分)
18.(本小题满分12分)本小题主要考查概率等基础知识,考查运算求解能力、应用数学知
识分析和解决实际问题的能力。
解:(Ⅰ)因 、
、 都可取1、2、3、4、5、6,
都可取1、2、3、4、5、6,
故以 为坐标的点共有36个 ………………………(2分)
为坐标的点共有36个 ………………………(2分)


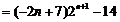 ………………………(12分)
………………………(12分)
22. (本小题满分14分)
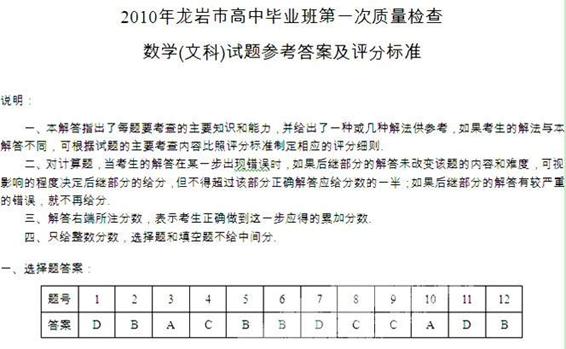
已知函数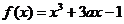 ,
,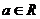 .
.
(Ⅰ)若函数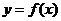 的图象在
的图象在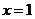 处的切线与直线
处的切线与直线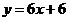 平行,求实数
平行,求实数 的值;
的值;
(Ⅱ)设函数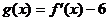 ,对满足
,对满足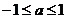 的一切
的一切 的值,都有
的值,都有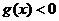 成立,
成立,
求实数 的取值范围;
的取值范围;
(Ⅲ)当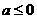 时,请问:是否存在整数
时,请问:是否存在整数 的值,使方程
的值,使方程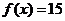 有且只有一个实根?若
有且只有一个实根?若
存在,求出整数 的值;否则,请说明理由.
的值;否则,请说明理由.

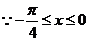 ,
,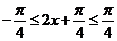
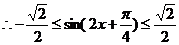
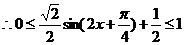 。
。
所以 的值域为
的值域为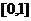 ………………………(12分)
………………………(12分)
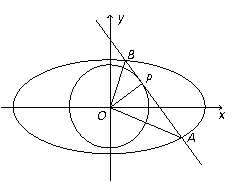
21.(本小题满分12分)
已知椭圆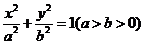 的离心率为
的离心率为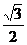 ,点
,点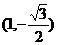 为椭圆上的一点,O为坐标原(Ⅰ)求椭圆的方程;
为椭圆上的一点,O为坐标原(Ⅰ)求椭圆的方程;
(Ⅱ)已知直线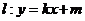 为圆
为圆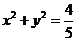 的切线,直线
的切线,直线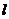 交椭圆于A、B两点,
交椭圆于A、B两点,
求证: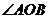 为直角。
为直角。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com