
11.________________________ 12.________________________
(18)(本题满分 分)已知向量
分)已知向量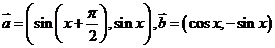 ,
,
函数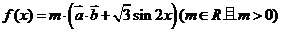 .
.
(Ⅰ)求函数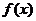 的最小正周期;
的最小正周期;
(Ⅱ)将函数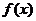 的图象的纵坐标保持不变,横坐标扩大到原来的两倍,然后再向右平移
的图象的纵坐标保持不变,横坐标扩大到原来的两倍,然后再向右平移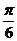 个单位得到
个单位得到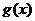 的图象,试探讨:当
的图象,试探讨:当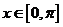 时,函数
时,函数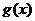 与
与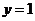 的图象的交点个数.
的图象的交点个数.
(19)(本题满分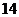 分)
分)
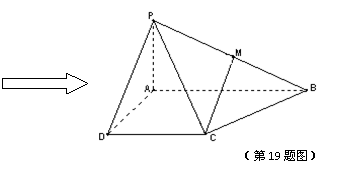
如图,在等腰梯形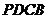 中,
中,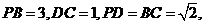
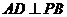 ,将
,将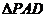 沿
沿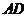 折起,使平面
折起,使平面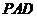 ⊥平面
⊥平面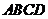 .
.
(Ⅰ)求证: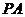 ⊥平面
⊥平面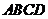 ;
;
(Ⅱ)求二面角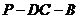 的大小;
的大小;
(Ⅲ)若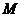 是侧棱
是侧棱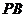 中点,求直线
中点,求直线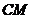 与平面
与平面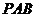 所成角的正弦值.
所成角的正弦值.
(20)(本题满分 分)
分)
数列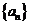 中,
中,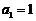 ,当
,当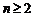 时,其前
时,其前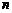 项的和
项的和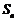 满足
满足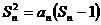 .
.
(Ⅰ)证明:数列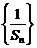 是等差数列;
是等差数列;
(Ⅱ)设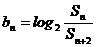 ,数列
,数列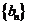 的前
的前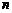 项和为
项和为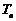 ,求满足
,求满足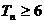 的最小正整数
的最小正整数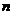 .
.
(21)(本题满分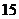 分)
分)
已知函数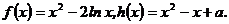
(Ⅰ)求函数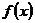 的极值;
的极值;
(Ⅱ)设函数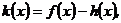 若函数
若函数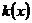 在
在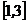 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数
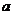 的取值范围.
的取值范围.
(22)(本题满分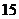 分)已知曲线
分)已知曲线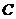 上的动点
上的动点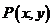 满足到点
满足到点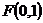 的距离比到直线
的距离比到直线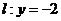 的距离小
的距离小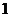 .
.
(Ⅰ)求曲线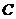 的方程;
的方程;
(Ⅱ)动点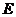 在直线
在直线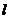 上,过点
上,过点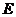 分别作曲线
分别作曲线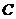 的切线
的切线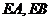 ,切点为
,切点为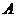 、
、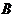 .
.
(ⅰ)求证:直线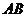 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;
(ⅱ)在直线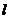 上是否存在一点
上是否存在一点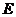 ,使得
,使得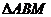 为等边三角形(
为等边三角形(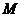 点也在直线
点也在直线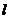 上)?若存在,求出点
上)?若存在,求出点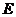 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.

 台州市2010年高三年级第一次调考试题
台州市2010年高三年级第一次调考试题
数 学(文) 答 题 卷 2010.3
(11)某赛季,甲乙两名篮球运动员都参加了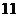 场比赛,他们每场
场比赛,他们每场
比赛得分的情况用右图所示的茎叶图表示,若
甲运动员的中位数为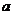 , 乙运动员的众数为
, 乙运动员的众数为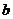 ,则
,则
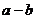 = ▲ .
= ▲ .
(12)在等比数列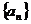 (
(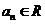 )
)
|
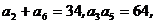
则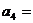 ▲ .
▲ .
(13)我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求
动点轨迹方程的方法,可以求出过点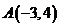 ,且法向量为
,且法向量为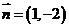 的直线(点法式)
的直线(点法式)
方程为: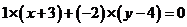 ,化简得
,化简得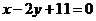 .类比以上方法,在空
.类比以上方法,在空
间直角坐标系中,经过点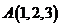 且法向量为
且法向量为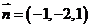 的平面(点法式)方程为:
的平面(点法式)方程为:
▲ .(请写出化简后的结果.)
(14)若直线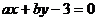 切圆
切圆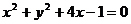 于点
于点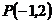 ,则
,则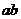 的值为 ▲ .
的值为 ▲ .
(15)甲盒子中装有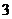 个编号分别为
个编号分别为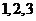 的小球,乙盒子中装有
的小球,乙盒子中装有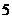 个编号分别为
个编号分别为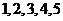 的小球,从甲、乙两个盒子中各随机取一个小球,则取出两小球编号之积为奇数的概率为
的小球,从甲、乙两个盒子中各随机取一个小球,则取出两小球编号之积为奇数的概率为
▲ .
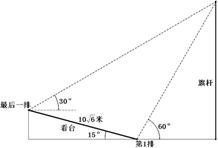 (16)某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度
(16)某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度
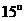 的看台的某一列的正前方,从这一列的第一排和最
的看台的某一列的正前方,从这一列的第一排和最
后一排测得旗杆顶部的仰角分别为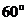 和
和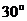 ,第一排
,第一排
和最后一排的距离为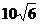 米(如图所示),旗杆底部
米(如图所示),旗杆底部
与第一排在一个水平面上.若国歌长度约为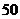 秒,升旗
秒,升旗
手应以 ▲ (米 /
|
(17)已知函数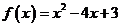 ,若实数
,若实数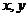 满足条件
满足条件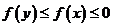 ,则
,则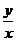 的取值范围为
▲ .
的取值范围为
▲ .
17.(14分) 长为6L、质量为6m的匀质绳,置于特制的水平桌面上,绳的一端悬垂于桌边外,另一端系有一个可视为质点的质量为M的木块,如图所示.木块在AB段与桌面无摩擦(E点位于桌子的边缘),在BE段与桌面有摩擦,匀质绳与桌面的摩擦可忽略.初始时刻用手按住木块使其停在A处,绳处于绷紧状态,AB = BC = CD = DE = L,放手后,木块最终停在C处.桌面距地面高度大于6L.
(1)求木块刚滑至B点时的速度v和木块与BE段的动摩擦因数μ;
(2)若木块在BE段与桌面的动摩擦因数变为μ′ = ,则木块最终停在何处?
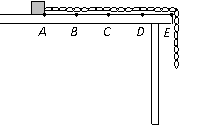 (3)是否存在一个μ值,能使木块从A处放手后,最终停在E处,且不再运动?若能,求出该μ值;若不能,简要说明理由.
(3)是否存在一个μ值,能使木块从A处放手后,最终停在E处,且不再运动?若能,求出该μ值;若不能,简要说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com