
5. 379班现有同学73人,要选取6名同学参加学校组织的膳食服务座谈会,班主任老师先随机排除一个同学,然后采用系统抽样的方法,从剩下的72名学生中抽取了6名,问班长被抽到的概率为( )
A
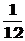 B
B 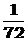 C
C 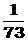 D
D 
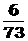
3.6个相同的小球放入标号为1、2、3的3个小盒中,要求每盒不空,共有放法种数为( )
A.8 B.10 C.6 D.60
4
将一枚质地均匀的骰子掷2次,第一次出现的点数记为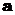 ,第二次出现的点数记为
,第二次出现的点数记为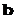 ,已知两条直线
,已知两条直线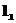 :
: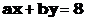 ,
,
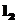 :
: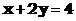 则两条直线相交的概率为( )
则两条直线相交的概率为( )
A 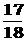 B
B 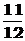 C
C 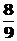 D
D 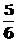
2.易建联在3月27日蓝网与活塞的比赛中,16投中12,保持此命中率不变,假设在下次比赛中有无限投篮权,那么他第一次投中时投篮次数的期望值为( )
A
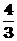 B 1 C
B 1 C 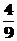 D
D 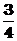 ^
^
1. 某自然保护区有12只大熊猫,从中捕捉5只做上标记,半年后,再从此保护区捕捉1只,则恰好此只带有标志的概率为( )
A 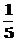 B
B 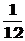 C
C 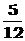 D
D 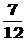
22. (本小题满分12分)
设函数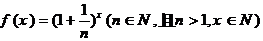 .
.
(1)当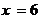 时,求
时,求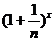 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(2)是否存在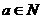 ,使得
,使得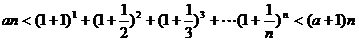 恒成立?若存在,试证明你的结论并求出
恒成立?若存在,试证明你的结论并求出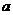 的值;若不存在,请说明理由.^
的值;若不存在,请说明理由.^
衡水中学2009-2010学年度第二学期期中考试
21.(本小题满分12分)甲、乙两队进行七局四胜制的比赛,即甲队或乙队谁先累计获胜四局比赛,即为冠军,若在每局比赛中,甲队获胜的概率为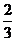 ,每局比赛必分出胜负,且每局比赛的胜负不影响下局的比赛。求(1)在第5局比赛结束后决出冠军的概率?
,每局比赛必分出胜负,且每局比赛的胜负不影响下局的比赛。求(1)在第5局比赛结束后决出冠军的概率?
(2)甲队获得冠军的概率?
^
20.(本小题满分12分)一个袋中有8个大小相同的小球,其中红球1个,白球和黑球若干,现从袋中有放回地取球,每次随机取一个,又知连续取两次都是白球的概率为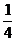 :
:
(1)求该口袋内白球和黑球的个数;
(2)若取一个红球记2分,取一个白球记1分,取一个黑球记0 分,连续取三次分数之和为4分的概率;
(3)现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有1人取得黑球时游戏终止,每个球在每一次被取出的机会均相同.求当游戏终止时,取球次数不多于3的概率。^
19. (本小题满分12分)某售货员负责在甲、乙、丙三个柜面上售货.如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8,0.7.假定各个柜面是否需要照顾相互之间没有影响,求在这个小时内:
(1)只有丙柜面需要售货员照顾的概率;
(2)三个柜面最多有一个需要售货员照顾的概率;
(3)三个柜面至少有一个需要售货员照顾的概率.^
18.(本小题满分12分)
某初级中学有三个年级,各年级男、女生人数如下表:
|
^ |
初一年级 |
初二年级 |
初三年级 |
|
女生 |
370^ |
z^ |
200^ |
|
男生 |
380 |
370 |
300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求z的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,将该样本看成一个总体,从中任选2名学生,求至少有1名女生的概率;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2, 1.5, 1.2, 1.5, 1.5, 1.3, 1.0, 1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
17.(本小题满分10分)求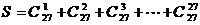 除以9的余数。^
除以9的余数。^
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com