S_△OBC= S_△OCF +S_△BCF==，

（3） 设存在点C（x , x²+x）（其中0<x<)，使四边形ABCO面积最大.

∵△OAB面积为定值，

∴只要△OBC面积最大，四边形ABCO面积就最大.

过点C作x轴的垂线CE，垂足为E，交OB于点F，则

∴ 所求二次函数解析式是 y=x²+x.

解方程组，有  a=，b=，c=0.

（2） 将A(2,0)、B()、O(0,0)三点的坐标代入y=ax²+bx+c，得

【思路点拨】（1） 在Rt△OAB中，∵∠AOB=30°，∴ OB=. 过点B作BD垂直于x轴，垂足为D，则  OD=，BD=，∴ 点B的坐标为() ．

【考点要求】本题考查求二次函数解析式，并探索抛物线上点的存在性，培养学生分析问题，解决问题的综合能力．

【答案】（1）；（2）如图3-5所示。

【方法点拨】本题的难点是对题目条件所给信息的理解与运用。突破方法：结合图形反复研读，理解不等式与它所对应的直线的关系，并能在图象中用阴影表示出来。运用这一知识求解不等式组时，也就是要找出各不等式所表示的阴影的公共部分。

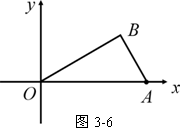
例11如图3-6，已知O为坐标原点，∠AOB=30°，∠ABO=90°，且点A的坐标

为（2,0）．

（1） 求点B的坐标；

（2） 若二次函数y=ax²+bx+c的图象经过A、B、O三点，求此二次函数的解析式；

（3） 在（2）中的二次函数图象的OB段（不包括点O、B）上，是否存在一点C，使得四边形ABCO的面积最大？若存在，求出这个最大值及此时点C的坐标；若不存在，请说明理由．

则是方程组的解．

（2）如阴影所示．