
22.动点P在x轴与直线l:y=3之间的区域(含边界)上运动,且到点F(0,1)和直线l的距离之和为4.
(1)求点P的轨迹C的方程;
(2)过点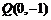 作曲线C的切线,求所作的切线与曲线C所围成区域的面积.
作曲线C的切线,求所作的切线与曲线C所围成区域的面积.
21. [选做题]在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
[选做题]在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
A.选修4-1 几何证明选讲
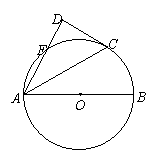
如图,AB是⊙O的直径,C、F为⊙O上的点,且CA平分∠BAF,过点C作CD⊥AF交AF的延长线于点D. 求证:DC是⊙O的切线.
B.选修4-2 矩阵与变换
变换T是绕坐标原点逆时针旋转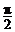 的旋转变换,求曲线
的旋转变换,求曲线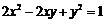 在变换T作用
在变换T作用
下所得的曲线方程.
C.选修4-4 参数方程与极坐标(本题满分10分)
已知圆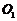 和圆
和圆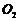 的极坐标方程分别为
的极坐标方程分别为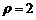 ,
,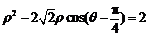 .
.
(1)把圆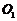 和圆
和圆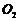 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
D.选修4-5 不等式证明选讲(本题满分10分)
已知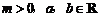 ,求证:
,求证: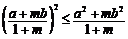 .
.
[必做题]第22题、第23题,每题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
20.(本小题满分16分)
已知二次函数g(x)对任意实数x都满足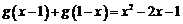 ,且
,且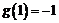 .令
.令
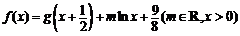 .
.
(1)求 g(x)的表达式;
(2)若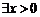 使
使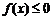 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)设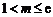 ,
,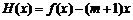 ,
,
证明:对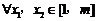 ,恒有
,恒有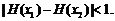
附加题部分
19.(本小题满分16分)已知椭圆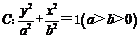 的离心率为
的离心率为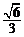 ,过右顶点A的直线l与椭圆C相交于A、B两点,且
,过右顶点A的直线l与椭圆C相交于A、B两点,且 .
.
(1)求椭圆C和直线l的方程;
(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若
曲线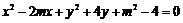 与D有公共点,试求实数m的最小值.
与D有公共点,试求实数m的最小值.
18.(本小题满分15分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,
已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个
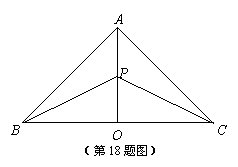 变电站.
记P到三个村庄的距离之和为y. (1)设
变电站.
记P到三个村庄的距离之和为y. (1)设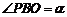 ,把y表示成
,把y表示成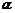 的函数关系式;
的函数关系式;
(2)变电站建于何处时,它到三个小区的距离之和最小?
17.(本小题满分15分)设等差数列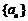 的前
的前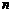 项和为
项和为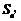 且
且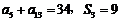 .
.
(1)求数列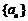 的通项公式及前
的通项公式及前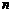 项和公式;
项和公式;
(2)设数列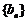 的通项公式为
的通项公式为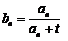 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得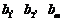
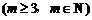 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
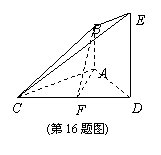
16.(本小题满分14分)如图,已知AB⊥平面ACD,DE⊥平面ACD,AC=AD,
DE=2AB,F为CD的中点.
(1) 求证:AF∥平面BCE;(2) 求证:平面BCE⊥平面CDE.
15.(本小题满分14分)在△ABC中,a,b,c分别是角A、B、C所对的边,且b2=ac,向量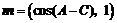 和
和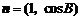 满足
满足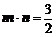 .
.
(1)求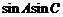 的值;(2)求证:三角形ABC为等边三角形.
的值;(2)求证:三角形ABC为等边三角形.
14.在平面直角坐标系xOy中,设直线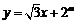 和圆
和圆 相切,其中m,
相切,其中m,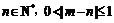 ,若函数
,若函数 的零点
的零点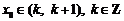 ,则k= ▲
.
,则k= ▲
.
13.设面积为S的平面四边形的第i条边的边长记为ai(i=1,2,3,4),P是该四边形内任意一点,P点到第i条边的距离记为hi,若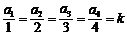 , 则
, 则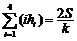 .类比上述结论,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),Q是该三棱锥内的任意一点,Q点到第i个面的距离记为Hi,则相应的正确命题是:若
.类比上述结论,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),Q是该三棱锥内的任意一点,Q点到第i个面的距离记为Hi,则相应的正确命题是:若 ,则 ▲ .
,则 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com