
1.了解平面向量基本定理,理解平面向量的坐标概念,会用坐标形式进行向量的加法、减法、数乘的运算,掌握向量坐标形式的平行的条件;
|

|
(四)巩固练习:《高考 计划》考点10智能训练6.
计划》考点10智能训练6.
(三)例题分析:
例1.判断下列各函数的奇偶性:
(1)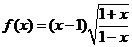 ;(2)
;(2)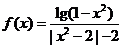 ;
;
(3)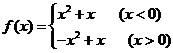 .
.
解:(1)由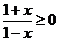 ,得定义域为
,得定义域为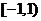 ,关于原点不对称,∴
,关于原点不对称,∴ 为非奇非偶函数.
为非奇非偶函数.
(2)由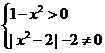 得定义域为
得定义域为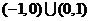 ,
,
∴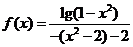
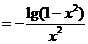 ,
,
 ∵
∵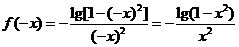
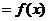 ∴
∴ 为偶函数
为偶函数
(3)当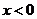 时,
时,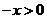 ,则
,则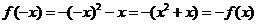 ,
,
当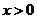 时,
时,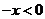 ,则
,则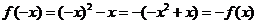 ,
,
综上所述,对任意的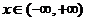 ,都有
,都有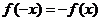 ,∴
,∴ 为奇函数.
为奇函数.
例2.已知函数 对一切
对一切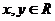 ,都有
,都有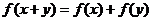 ,
,
(1)求证: 是奇函数;(2)若
是奇函数;(2)若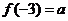 ,用
,用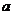 表示
表示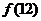 .
.
解:(1)显然 的定义域是
的定义域是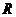 ,它关于原点对称.在
,它关于原点对称.在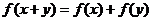 中,
中,
令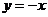 ,得
,得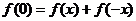 ,令
,令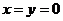 ,得
,得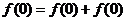 ,
,
∴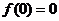 ,∴
,∴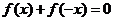 ,即
,即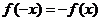 , ∴
, ∴ 是奇函数.
是奇函数.
(2)由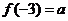 ,
,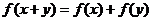 及
及 是奇函数,
是奇函数,
得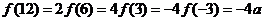 .
.
例3.(1)已知 是
是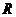 上的奇函数,且当
上的奇函数,且当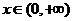 时,
时,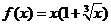 ,
,
则 的解析式为
的解析式为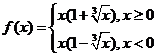 .
.
(2) (《高考 计划》考点3“智能训练第4题”)已知
计划》考点3“智能训练第4题”)已知 是偶函数,
是偶函数,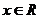 ,当
,当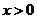 时,
时, 为增函数,若
为增函数,若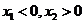 ,且
,且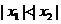 ,则
(
,则
( 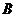 )
)
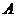 .
.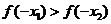
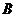 .
.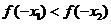
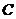 .
.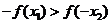
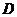 .
. 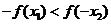
例4.设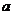 为实数,函数
为实数,函数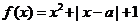 ,
,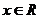 .
.
(1)讨论 的奇偶性; (2)求
的奇偶性; (2)求  的最小值.
的最小值.
解:(1)当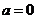 时,
时,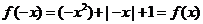 ,此时
,此时 为偶函数;
为偶函数;
当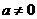 时,
时,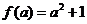 ,
,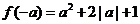 ,
,
∴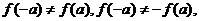
此时函数 既不是奇函数也不是偶函数.
既不是奇函数也不是偶函数.
(2)①当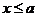 时,函数
时,函数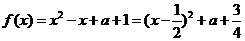 ,
,
若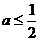 ,则函数
,则函数 在
在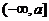 上单调递减,∴函数
上单调递减,∴函数 在
在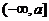 上的最小值为
上的最小值为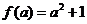 ;
;
若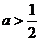 ,函数
,函数 在
在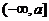 上的最小值为
上的最小值为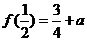 ,且
,且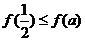 .
.
②当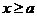 时,函数
时,函数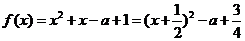 ,
,
若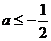 ,则函数
,则函数 在
在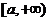 上的最小值为
上的最小值为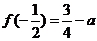 ,且
,且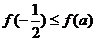 ;
;
若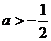 ,则函数
,则函数 在
在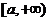 上单调递增,∴函数
上单调递增,∴函数 在
在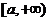 上的最小值
上的最小值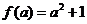 .
.
综上,当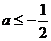 时,函数
时,函数 的最小值是
的最小值是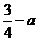 ,当
,当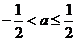 时,函数
时,函数 的最小值是
的最小值是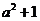 ,
,
当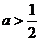 ,函数
,函数 的最小值是
的最小值是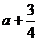 .
.
例5.(《高考 计划》考点3“智能训练第15题”)
计划》考点3“智能训练第15题”)
已知 是定义在实数集
是定义在实数集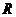 上的函数,满足
上的函数,满足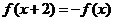 ,且
,且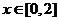 时,
时,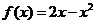 ,
,
(1)求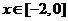 时,
时, 的表达式;(2)证明
的表达式;(2)证明 是
是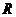 上的奇函数.
上的奇函数.
(参见《高考 计划》教师用书
计划》教师用书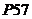 )
)
(二)主要方法:
1.判断函数的奇偶性,首先要研究函数的定义域,有时还要对函数式化简整理,但必须注意使定义域不受影响;
2.牢记奇偶函数的图象特征,有助于判断函数的奇偶性;
3.判断函数的奇偶性有时可以用定义的等价形式: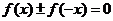 ,
,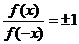 .
.
4.设 ,
,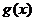 的定义域分别是
的定义域分别是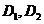 ,那么在它们的公共定义域上:
,那么在它们的公共定义域上:
奇+奇=奇,奇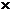 奇=偶,偶+偶=偶,偶
奇=偶,偶+偶=偶,偶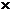 偶=偶,奇
偶=偶,奇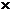 偶=奇.
偶=奇.
5.注意数形结合思想的应用.
(一)主要知识:
1.函数的奇偶性的定义;
2.奇偶函数的性质:
(1)定义域关于原点对称;(2)偶函数的图象关于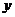 轴对称,奇函数的图象关于原点对称;
轴对称,奇函数的图象关于原点对称;
3. 为偶函数
为偶函数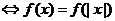 .
.
4.若奇函数 的定义域包含
的定义域包含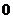 ,则
,则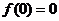 .
.
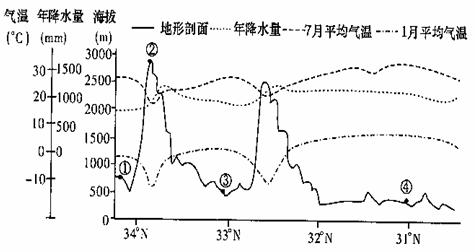
25.1月,④地气温高于③地的原因除纬度因素外,主要是因为④地
A.海拔较高 B.受夏季风影响较大
C.森林覆盖率高 D.受冬季风影响较小
2009-2010(下)巴中市四县中期末联考高2011级

 地理试题
地理试题
24.图中①地的气温年较差为
A.10℃ B.20℃ C.30℃ D.40℃
23.图中山地②年降水量最多的海拔高度大约位于
A.山顶2900米处 B.南坡海拔2300米处
C.南坡海拔2500米处 D.北坡海拔2100米处
22.杭州到深圳的沿海铁路对途经港口的发展具有重要意义,对此理解正确的是

 *
*
①加快城市化、工业化进程 ②扩大港口的经济腹地
③提高人们生活质量 ④增强港口的综合运输能力
A.①③ B.①④ C.②③ D.②④
下图是“沿106.5°E经线的地形剖面及相关气候资料图”,据图回答23-25题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com