
(三)例题分析:
例1.(1)求函数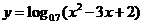 的单调区间;
的单调区间;
(2)已知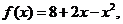 若
若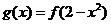 试确定
试确定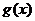 的单调区间和单调性.
的单调区间和单调性.
解:(1)单调增区间为: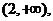 单调减区间为
单调减区间为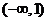 ,
,
(2)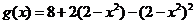
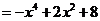 ,
,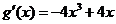 ,
,
令 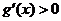 ,得
,得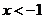 或
或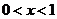 ,令
,令 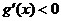 ,
,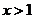 或
或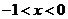
∴单调增区间为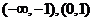 ;单调减区间为
;单调减区间为 .
.
例2.设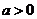 ,
,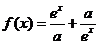 是
是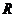 上的偶函数.
上的偶函数.
(1)求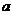 的值;(2)证明
的值;(2)证明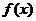 在
在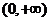 上为增函数.
上为增函数.
解:(1)依题意,对一切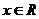 ,有
,有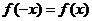 ,即
,即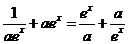
∴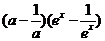
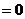 对一切
对一切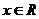 成立,则
成立,则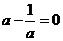 ,∴
,∴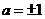 ,∵
,∵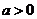 ,∴
,∴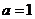 .
.
(2)设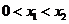 ,则
,则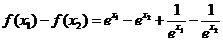
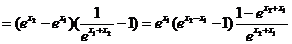 ,
,
由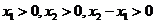 ,得
,得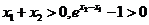 ,
,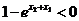 ,
,
∴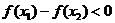 ,
,
即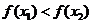 ,∴
,∴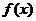 在
在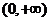 上为增函数.
上为增函数.
例3.(1)(《高考 计划》考点11“智能训练第9题”)若
计划》考点11“智能训练第9题”)若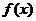 为奇函数,且在
为奇函数,且在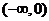 上是减函数,又
上是减函数,又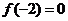 ,则
,则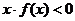 的解集为
的解集为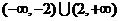 .
.
例4.(《高考 计划》考点10智能训练14)已知函数
计划》考点10智能训练14)已知函数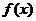 的定义域是
的定义域是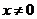 的一切实数,对定义域内的任意
的一切实数,对定义域内的任意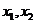 都有
都有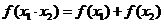 ,且当
,且当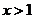 时
时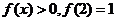 ,
,
(1)求证: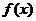 是偶函数;(2)
是偶函数;(2)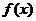 在
在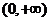 上是增函数;(3)解不等式
上是增函数;(3)解不等式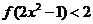 .
.
解:(1)令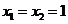 ,得
,得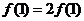 ,∴
,∴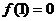 ,令
,令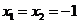 ,得∴
,得∴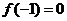 ,
,
∴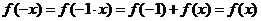 ,∴
,∴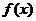 是偶函数.
是偶函数.
(2)设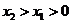 ,则
,则
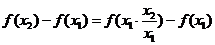
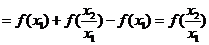
∵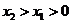 ,∴
,∴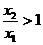 ,∴
,∴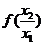
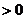 ,即
,即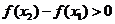 ,∴
,∴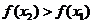
∴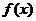 在
在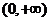 上是增函数.
上是增函数.
(3)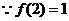 ,∴
,∴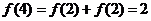 ,
,
∵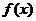 是偶函数∴不等式
是偶函数∴不等式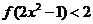 可化为
可化为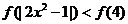 ,
,
又∵函数在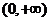 上是增函数,∴
上是增函数,∴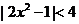 ,解得:
,解得: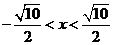 ,
,
即不等式的解集为 .
.
例5.函数 在
在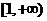 上是增函数,求
上是增函数,求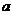 的取值范围.
的取值范围.
分析:由函数 在
在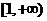 上是增函数可以得到两个信息:①对任意的
上是增函数可以得到两个信息:①对任意的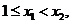 总有
总有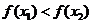 ;②当
;②当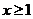 时,
时,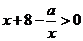 恒成立.
恒成立.
解:∵函数 在
在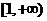 上是增函数,∴对任意的
上是增函数,∴对任意的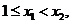 有
有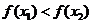 ,即
,即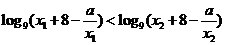 ,得
,得
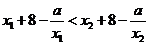 ,即
,即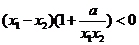 ,
,
∵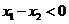 ,∴
,∴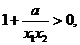
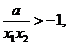
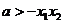 ,
,
∵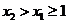 ,∴要使
,∴要使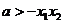 恒成立,只要
恒成立,只要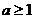 ;
;
又∵函数 在
在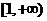 上是增函数,∴
上是增函数,∴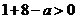 ,
,
即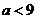 ,综上
,综上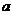 的取值范围为
的取值范围为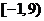 .
.
另解:(用导数求解)令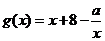 ,函数
,函数 在
在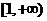 上是增函数,
上是增函数,
∴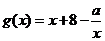 在
在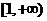 上是增函数,
上是增函数,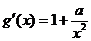 ,
,
∴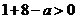 ,且
,且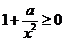 在
在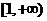 上恒成立,得
上恒成立,得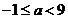 .
.
(二)主要方法:
1.讨论函数单调性必须在其定义域内进行,因此要研究函数单调性必须先求函数的定义域,函数的单调区间是定义域的子集;
2.判断函数的单调性的方法有:(1)用定义;(2)用已知函数的单调性;(3)利用函数的导数.
3.注意函数的单调性的应用;
4.注意分类讨论与数形结合的应用.
(一)主要知识:
1.函数单调性的定义;
2.判断函数的单调性的方法;求函数的单调区间;
3.复合函数单调性的判断.
20.(本小题满分12分)
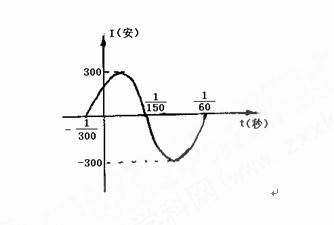
如图,表示电流强度I与时间t的关系式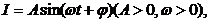 在一个周期内的图像
在一个周期内的图像
(1)根据图像写出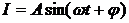 的解析式;
的解析式;
(2)为了使 中t在任意一段
中t在任意一段 秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数
秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数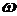 的最小值为多少?
的最小值为多少?
延安市实验中学2009-2010学年度第二学期中期
19.(本小题满分12分)
求函数 的定义域、值域、单调性、周期性、最值.
的定义域、值域、单调性、周期性、最值.
18.(本小题满分10分)
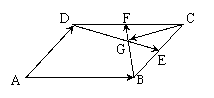 如图,
如图,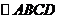 中,
中,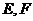 分别是
分别是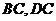 的中点,
的中点, 为交点,若
为交点,若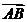 =
=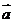 ,
,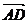 =
= ,试以
,试以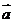 ,
, 为基底表示
为基底表示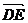 、
、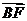 、
、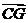 .
.
17.(本小题10分)已知函数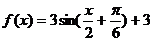
(1)用五点法画出它在一个周期内的闭区间上的图像;
(2)指出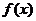 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图像可由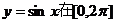 上的图像经怎样的变换得到.
上的图像经怎样的变换得到.

16、(本小题10分)
(1)化简: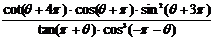
(2)已知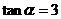 ,计算
,计算 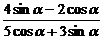 的值
的值
15.(本小题6分)已知A(1,0),B(4,3),C(2,4),D(0,2),试证明四边形ABCD是梯形。
14.给出下列命题:(1)存在实数x,使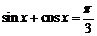 ; (2)若
; (2)若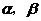 是锐角△
是锐角△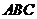 的内角,则
的内角,则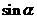 >
>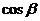 ; (3)函数
; (3)函数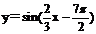 是偶函数; (4)函数y=sin2x的图像向右平移
是偶函数; (4)函数y=sin2x的图像向右平移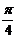 个单位,得到y=sin(2x+
个单位,得到y=sin(2x+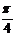 )的图像.其中正确的命题的序号是
.
)的图像.其中正确的命题的序号是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com